二次函数的概念及y=ax^2(a≠0）、y=ax^2+c(a≠0）的图象与性质

重难点

1． 掌握二次函数的概念，会用二次函数的定义识别二次函数，能根据实际问题列出简单的二次函数关系式；

2.用类比的方法学习二次函数几种常见的解析式之间的性质．会应用相关的性质解题。

例题精讲

模块一 二次函数的定义

1. 一般地，形如y=ax^2+bx+c（a/b/c为常数，a≠0）的函数称为x的二次函数，其中x为自变量，y为因变量，a/b/c分别为二次函数的二次项、一次项和常数项系数．

2. 任何二次函数都可以整理成y=ax^2+bx+c（a/b/c为常数，a≠0）的形式．

3. 判断函数是否为二次函数的方法：

① 含有一个变量，且自变量的最高次数为2；

② 二次项系数不等于0；

③ 等式两边都是整式．

4.二次函数自变量x的取值范围是全体实数．

【例1】 下列函数中是二次函数的是（ ）

A． y=1/(x^2+x+1) B．y=x^3+5x^2

C． y=(x-5)^2-x^2 D．y=2x-7x^2

【难度】1星

【解析】首先选出整式函数，再整理成一般形式，根据二次函数的定义条件判定即可

【答案】D

【例2】 下列说法正确的是（ ）

A．二次函数的自变量的取值范围是非零实数

B．圆的面积公式s=πr^2中，s是r的二次函数

C．y=(x-1)(x+6)不是二次函数

D．y=6-4x^2中一次项系数为1

【难度】1星

【解析】考查二次函数的基本知识点。

【答案】B

模块二 二次函数y=ax^2(a≠0）的图象与性质

1. 顶点坐标：原点（0，0）

2. 对称轴：x=0，或说y轴

3. 图象：抛物线

4. 图象与a的符号关系：

① 当a＞0时<=>抛物线开口向上<=>顶点为其最低点；

② 当a＞0时<=>抛物线开口向下<=>顶点为其最高点.

5. 抛物线的开口大小与|a|有关，|a|越大，开口越小；|a|越小，开口越大。

6. 二次函数y=ax^2(a≠0）性质对比

当a＞0时

开口向上，顶点坐标（0,0）对称轴y轴

x＞0时，y随x的增大而增大；

x＜0时，y随x的增大而减小；

x=0时，y有最小值0；

当a＜0时

开口向下，顶点坐标（0,0）对称轴y轴

x＞0时，y随x的增大而减小；

x＜0时，y随x的增大而增大；

x=0时，y有最大值0；

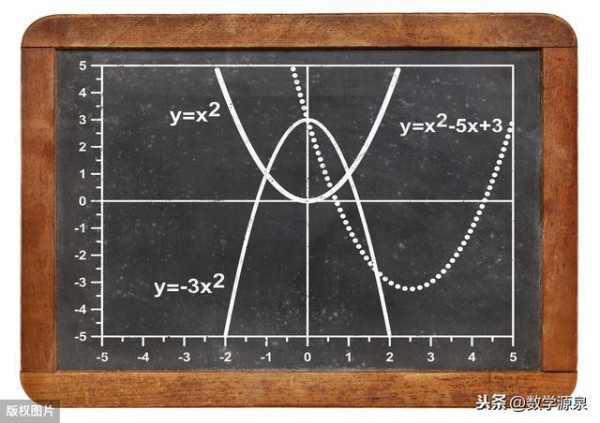
【例3】 在同一平面直角坐标系中作出下列函数图象：y=2x^2；y=-2x^2；y=3x^2；y=-3x^2；并探究二次函数开口大小与a之间的关系

【难度】2星

【解析】作图要按照列表、描点、连线的方法来做；二次函数作图象要用五点法，自变量要既取正数，又取负数。

【答案】列表略，图略

【小结】抛物线的开口方向与a的符号有关，当a＞0时，开口向上；a＜0时，开口向下；

抛物线的开口大小与|a|有关，|a|越大，开口越小；|a|越小，开口越大。

(2016·玉林)抛物线y＝0.5x^2，y＝x^2，y＝－x^2的共同性质：① 都是开口向上；② 都以点(0，0)为顶点；③ 都以y轴为对称轴；④ 都关于x轴对称．其中正确的有(　　)

A. 1个　　B. 2个　C. 3个　D. 4个

模块三 二次函数y=ax^2+c(a≠0）的图象与性质

1. 顶点坐标：原点（0，c）

2. 对称轴：x=0（ y轴）

3. 函数y=ax^2+c的图像与a的符号关系：

① 当a＞0时<=>抛物线开口向上<=>顶点为其最低点；

② 当a＜0时<=>抛物线开口向下<=>顶点为其最高点.

4. 函数y=ax^2+c的图像可以看做是y=ax^2由函数的图像向上或向下平移|c|个单位得到的；c＞0时，向上平移；c＜0时，向下平移。

5. c决定了函数图象与y轴的交点坐标：(0,c)

【例4】 函数y=2x^2-3的图象可以看做y=2x^2是函数的图象向 平移 个单位得到的。

【难度】1星

【解析】考查函数y=ax^2+c与y=ax^2之间的关系。

【答案】向下平移3个单位

(2018·淮安)将二次函数y＝x2－1的图象向上平移3个单位长度，得到的图象所对应的函数解析式是__________

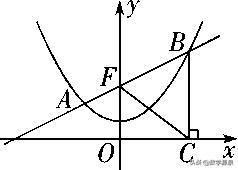
(2017·恩施州)如图，抛物线y＝ax2＋c过点(－2，2)，(4，5)，过y轴上定点F的直线l：y＝kx＋2与抛物线交于A，B两点，点B在点A的右侧，过点B作x轴的垂线，垂足为C.

(1) 求抛物线对应的函数解析式；

(2) 当点B在抛物线上运动时，判断线段BF与BC的数量关系，并证明你的判断；

(3) P为y轴上一点，若以B，C，F，P为顶点的四边形是菱形，设点P(0，m)，求自然数m的值．

特别声明：以上内容(如有图片或视频亦包括在内)为自媒体平台“网易号”用户上传并发布，本平台仅提供信息存储服务。

Notice: The content above (including the pictures and videos if any) is uploaded and posted by a user of NetEase Hao, which is a social media platform and only provides information storage services.

网址：二次函数的概念及y=ax^2(a≠0）、y=ax^2+c(a≠0）的图象与性质 https://mxgxt.com/news/view/179768

相关内容

已知z=f(2xy,x^2+y^2,x^3)，且z对x,y的所有二阶偏导数
数学初一上册1、观察下列等式：7的1次方=7，7的2次方=49， 爱问知识人
下列函数关系y中.变量y与x成正比例函数关系的是( ) A.y=x2 B.y= C.y=x
y=x^3导数y'=3x^2这个求解过程是？ 爱问知识人
为了响应政府提出的由中国制造向中国创造转型的号召，某公司自主设计了一款成本为40元的可控温杯，并投放市场进行试销售，经过调查发现该产品每天的销售量y（件）与销售单价x（元）满足一次函数关系：y=﹣10x+1200．
r=a(1
sin(A/2)=√((1
剖析C语言中a=a+++++a的无聊问题
关于明星投票系统的作业分享
手把手教你用几行Python和消费数据做客户细分

随便看看