菲尔兹奖近在咫尺？陶哲轩盛赞王虹，百年难题究竟如何被破解？

发布时间：2025-08-09 21:14

当2006年菲尔兹奖得主、数学界泰斗级人物陶哲轩在个人博客上盛赞一位年仅34岁的华裔女数学家王虹的工作时，无数人的目光聚焦在了她和她与不列颠哥伦比亚大学副教授Joshua Zahl共同完成的一项惊人成果上。

“There has been some spectacular progress in geometric measure theory: Hong Wang and Joshua Zahl have just released a preprint that resolves the three-dimensional case of the infamous Kakeya set conjecture!”

——Terence Tao

陶哲轩甚至用“壮观进展”(spectacular progress )来形容这项突破，并认为它解决了数学领域一个“臭名昭著”的猜想。许多人猜测，凭借这项划时代的成就，王虹极有可能在明年举行的国际数学家大会上摘得菲尔兹奖的桂冠。

王虹所任教的纽约大学库朗研究所的数学系主任 Eyal Lubetzky评价王虹的成就说：“它是 21 世纪最顶尖的数学成就之一。”

“It stands as one of the top mathematical achievements of the 21st century.”

——Eyal Lubetzky

那么，究竟是什么样的难题，能让如此重量级的数学家们给出如此高的评价？王虹和她的合作者攻克的，是困扰了数学界整整一百年的“挂谷猜想”（Kakeya conjecture）。

挂谷

猜想

这个猜想的起源非常简单，简单到中学生都能理解：想象一下，你手里拿着一根细细的针，你想在平面的任何方向都能让这根针指到，你需要多大的面积才能做到呢？

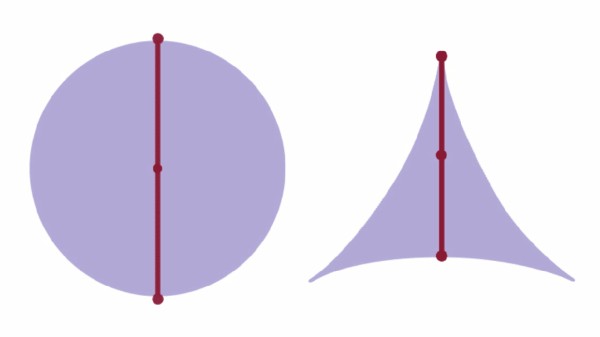
一个显而易见的答案是让针在一个圆内旋转，但这并非最优解。挂谷本人提出，更优的方案是利用一个被称为“星形区域”的几何形状，比如一个三尖瓣的内摆线。然而，数学家们很快发现，如果不对区域的形状加以限制（比如必须是凸的），那么这个面积可以无限趋近于零.

想象一下，你手里有一根细细的针。现在，你想让这根针在平面的任何方向都能指到，你需要多大的地方才能做到呢？一个简单的方法是画一个圆，让针在里面转，但这并不是最好的方法。一百多年前，一位聪明的日本数学家挂谷宗一提出了这个问题。他想知道，到底需要最小多大的面积，才能让一根单位长度的针在平面上自由地旋转360度，指向任何方向？

后来，数学家们把这个问题变得更难了，他们想：如果在三维空间里，我们有一根可以指向任何方向的“线段”（你可以想象成一根无限细的筷子），那么包含所有这些线段的集合，它的大小（或者说体积）最小会是多少呢？这就是著名的“挂谷猜想”（Kakeya conjecture）的核心问题。数学家们猜测，在三维空间里，这个集合的大小必须和整个三维空间一样“大”，也就是说，你不可能用一个非常非常小的体积就能包含所有方向的线段。

这个问题在二维空间里已经被解决了，答案是这样的集合可以非常非常小，面积可以无限接近于零。但是，在三维或者更高的空间里，这个问题就像一个神秘的谜题，难倒了无数聪明的数学家。

终于，在2025年2月，两位杰出的数学家——一位是34岁的中国女数学家王虹，另一位是加拿大不列颠哥伦比亚大学的副教授Joshua Zahl ，他们共同完成了一篇长达127页的论文，宣布他们找到了这个百年难题的答案！。这个消息让整个数学界都沸腾了，大家都觉得王虹很有可能获得数学界的最高荣誉——菲尔兹奖。

王虹从小就是个学霸，她小学的时候就跳过两级，16岁就考上了北京大学。后来她去了法国和美国继续深造，最终在麻省理工学院获得了博士学位。现在，她在纽约大学柯朗数学科学研究所担任副教授。王虹说，她觉得挂谷猜想很有意思，因为它看起来很简单，但却非常难解决。

“You have these concrete things you can visualize. It’s not as scary as other math theories. I just wanted to understand why it’s hard.”

——Wang Hong

她的搭档Joshua Zahl也是一位非常厉害的数学家，他对这个问题也很感兴趣。他们一起努力，终于找到了解决这个难题的方法。

他们的论文主要研究了三维空间里一种叫做“δ-管”（δ-tubes）的东西。你可以想象这些“δ-管”是非常细长的圆柱体，它们指向不同的方向。王虹和Zahl证明，如果这些细管的集合不是“挤”在一起的（也就是说，没有太多的细管挤在一个小的区域里），那么这些细管加起来的体积就必须很大，几乎达到最大可能的值。

通过这个重要的发现，他们成功地证明了在三维空间里，任何包含所有方向线段的集合，它的大小都必须是“完整”的，也就是说，它的维度必须是3 。

为了更好地理解他们的证明，你可以想象挂谷集就像一堆“生意大利面条”，它们长度一样，但是非常细，而且可以互相重叠，指向不同的方向。在二维空间里，我们可以用几乎是零的面积来包含所有方向的“面条”。但是在三维空间里，王虹和Zahl证明了，你不可能用一个无限小的体积来做到这一点。

他们用了一种叫做“多尺度分析”的聪明方法，把复杂的问题分解成很多小部分来研究，然后再把这些小部分组合起来，从而解决了整个问题。他们没有直接研究无限细的线段，而是研究了非常细但有一定厚度的“δ-管”。

他们的证明过程就像一个接力赛，他们先证明了一个简单的情况，然后一步一步地推导出更复杂的情况，最终完成了整个证明。他们还引入了一些新的数学概念，比如“谷物”（grains），把空间分割成很多小区域，然后分析这些小区域里“管”的相交方式。他们还创造了三种特殊的操作来处理这些“谷物”，就像玩积木一样，通过分裂、合并和移动这些“谷物”，让他们能够更好地理解“管”的排列方式。

这个数学上的重大突破不仅仅解决了一个百年难题，它还和数学的其他领域，比如调和分析，有着很深的联系。调和分析是研究怎么把复杂的函数分解成简单函数的和。挂谷猜想是调和分析里一个很重要的基础问题。王虹和Zahl的证明，为这个数学领域打下了更坚实的基础，有望帮助数学家们解决更多相关的难题。

更令人兴奋的是，这个看似很抽象的数学成果，可能在我们的生活中有很多实际应用。比如，在市场分析方面，分析师需要考虑消费者的各种行为。王虹和Zahl分析挂谷集的方法，可以帮助我们更好地分析高维数据，找到隐藏的规律，从而改进广告和推荐系统。在无线通信领域，理解信号在各个方向的传播方式对于设计更好的网络非常重要。他们的研究成果可能会帮助我们设计出更快的无线技术。甚至在医学成像领域，比如核磁共振成像（MRI），也可能用到他们的方法。

王虹和Zahl的成功不是偶然的，他们的工作建立在很多前辈数学家的研究基础上。比如，菲尔兹奖得主陶哲轩也对这个问题做出了重要的贡献。

为解决猜想做出贡献的关键人物：