函数y=1/(x+2)的主要性质与图像

函数y=1/(x+2)的主要性质与图像

主要内容：

本题主要介绍函数y=1/(x+2)的定义域、值域、单调性、凸凹性、极限等性质，并通过函数导数知识求解函数的单调区间和凸凹区间。

函数的定义域：

该函数y=1/(x+2)为分式函数，要求分母不为0，

因为x+2≠0，则x≠-2,故函数的定义域为：

(-∞,-2)，(-2,+∞)。

函数的单调性：

因为函数为分式函数，分子为常数，所以函数的单调性与分母函数的单调性相反。

对于分母函数g(x)=x+2，为一次函数，且为增函数。

所以函数y=1/(x+2)为减函数。

导数单调性：

因为y=1/(x+2)，对x求导，所以有：

dy/dx=-1/(x+2)^2，可知dy/dx<0，

即函数y为单调减函数。

从复合函数性质来看，y=1/(x+2)为复合反比例函数，由反比例函数y=1/x平移变形得到。

函数的凸凹性：

由dy/dx=-1/(x+2)^2得：

dy/dx=-(x+2)^(-2)，再次对x求导，有：

d^2y/dx^2=-(-2)(x+2)^(-3)=(x+2)^(-3),

则d^2y/dx^2=1/(x+2)^3，

该二次导数的间断点为x=-2，即：

(1)当x∈(-∞，-2)时，d^2y/dx^2<0,则函数y为凸函数。

(2当x∈(-2,+∞)时，d^2y/dx^2>0则函数y为凹函数。

函数的极限：

lim(x→-∞) 1/(x+2)=0；

lim(x+→-2/1) 1/(x+2)=+∞；

lim(x-→-2/1) 1/(x+2)=-∞；

lim(x→+∞) 1/(x+2)=0。

函数的五点示意图如下：

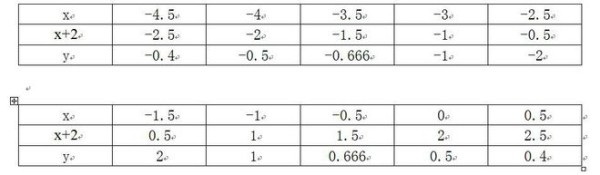
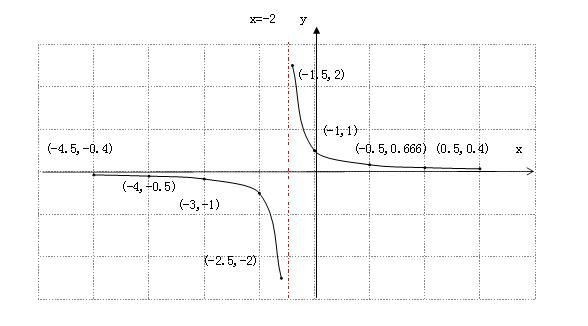
综合以上函数的性质，该函数的示意图大致如下所示。

特别声明：以上内容(如有图片或视频亦包括在内)为自媒体平台“网易号”用户上传并发布，本平台仅提供信息存储服务。

Notice: The content above (including the pictures and videos if any) is uploaded and posted by a user of NetEase Hao, which is a social media platform and only provides information storage services.

白话拆解｜是谁让美国两大港口“无人问津”？

国际在线

2025-05-07 17:09:27

一种叫得出却写不出名字的蔬菜——ong菜

亭里说事

2025-05-07 15:47:25

网址：函数y=1/(x+2)的主要性质与图像 https://mxgxt.com/news/view/1058620

相关内容

函数y=(x+1)/√2x+1的主要性质
解析函数y=(x+3)^2(3x+19)^3的主要性质
曲线x^3+y^3=1的主要性质
二次函数的概念及y=ax^2(a≠0）、y=ax^2+c(a≠0）的图象与性质
求解函数y=√2
下列函数关系y中.变量y与x成正比例函数关系的是( ) A.y=x2 B.y= C.y=x
函数xy=2与直线y=
y=(x+1)sin2x+cos^3(2x+1)的导数
二重积分1.设I1=∫∫（x^2+y^2)^3dσ.其中D1={ 爱问知识人
已知z=f(2xy,x^2+y^2,x^3)，且z对x,y的所有二阶偏导数

随便看看