研究方法

摘要：大规模问卷调查需要考虑诸多因素。研究者希望通过以尽可能少的成本投入获得足够精确且充分详细的调查数据信息，并在有效数据基础上，通过恰当的统计方法挖掘变量间关系。但是，大规模问卷调查抽取的样本需要符合总体结构分布，调查对象往往具有不同的结构特征，于是需要借助样本量分配、问卷设计以及多水平关系测度开展相关研究。本文紧密围绕样本的总体结构特征，从样本量测算与分配方法、问卷分割技术、多水平关系量化方法三个方面探讨大规模问卷调查统计方法，旨在为社会各界和政府等相关部门提供建议与参考。

关键词：大数据，样本量测算，问卷分割设计，多水平关系

一项大规模问卷调查的设计需要考虑诸多因素。在大数据背景下，首先需要招募和选择覆盖一定范围、满足结构特征的海量被调查对象，其次对被调查者信息的需求更为细致、问卷题量更为巨大。于是，大规模问卷调查往往形成一份较长的问卷和较大的发放数量，因此需要每位被调查对象投入更多时间和精力接受问卷调查。相应地，大规模问卷调查工作的开展需要更多人力、物力和财力加以支持。

研究者总是希望获取反映被调查者全体的、足够精确且充分详细的调查数据信息。这意味着大规模问卷调查需要足够大的样本量（减小抽样误差）和足够好的测量工具（减小观测误差）。但是，实际经验和已有研究表明，样本量与投入成本（人力、物力和财力）呈正相关，问卷的篇幅与数据质量呈负相关。这是因为，每发放一份问卷，都需要提供配套的时间、调查资源和资金支持，冗长的问卷容易造成被调查对象的疲惫感，产生消极情绪，从而增加问卷拒访率、无填答率和错答率。即便在收到问卷调查数据后，进行数据清理、删除无效问卷，也可能因为被调查对象的疲惫和反感而降低有效问卷数据的质量。尤其在数字经济时代，人们的工作、生活节奏加快，时间存在高度碎片化的特征，被调查者很容易出现拒答、错答和中途退答的情况。因此，在现代社会背景下，大规模问卷调查更需要克服调查成本、问卷体量等方面带来的诸多挑战。科学制定样本量、基于结构特征进行问卷分割是克服调查成本、问卷题量庞杂的有效途径。

此外，大规模问卷调查往往涉及不同调查对象群体（即被调查对象具有异质性），比如，一线城市、二线城市以及边缘地区等等。受经济、文化因素的影响，被调查者在不同时间和情境下回答同一问题时往往会有不同的答案，这时通过调查问卷回收的有效调查数据分析，需要考虑不同水平下变量间关系的差异化问题。因此，多水平关系量化对于测度不同题目间关系非常有帮助。它能够刻画出不同水平下一个变量随另一个变量的变化情况，同时勾勒出大规模问卷调查背景下变量间关系的全貌。

综上所述，本文主要讨论兼顾总体结构特征的样本量测算与分配方法、基于结构特征的问卷分割设计以及多水平关系量化方法三个方面的研究问题。

1. 兼顾总体结构特征的样本量测算与分配方法

1.1 样本量测算方法

本文讨论的样本量测算需要考虑总体的结构特征（比如，不同地域分布特征、不同职业类型特征，等等），以保证样本能够充分代表总体。但是，这并不意味着样本量越大越好，过大的样本量需要过多的成本投入。有时，实际可获取的样本量会受到客观有限资源（比如，调查费用、调查访员数量）的限制，可能无法满足巨大的样本量需求。相反，过小的样本量则会导致所获取样本无法覆盖总体的所有结构特征，造成抽样误差增大，影响抽样推断的可靠程度。综合考虑，样本量测算可参考Cochran样本量测算模型：n=Z2α/2p(1-p)/E2。其中，α表示显著性水平，Zα/2表示Z统计量，p表示概率值，E表示误差值[1]。

不妨假设问卷有效率为r，则本文样本量（记为s）的测算方法为：

通常，显著性水平α为0.01和0.05，对应地，统计量Zα/2取值为2.58和1.96。概率值p可以考虑p(1-p)达到最大值的情况，即p为0.5。为了尽可能保证测算的精确性，误差限E为0.01。问卷有效率r与调查渠道与方式、问卷容量与质量等诸多因素相关，通常通过预调查获得问卷有效率r的具体取值。根据某项已开展的电话预调查结果，有效问卷率为20%。本文假定问卷的有效回收率为20%，当显著性水平α为0.01时，样本量初步估计为：s=2.582*0.25/(0.20*0.012)=83205；当显著性水平α为0.05时，样本量初步估计为：s=1.962*0.25/(0.20*0.012)=48020。

由样本量测算公式可知，样本量的测算并未考虑具体研究对象特征，更未涉及总体结构特征信息。因此，针对需要进一步结合被调查对象的结构特征信息和预调查的结果，估计出问卷有效率，并合理分配样本，以符合总体结构特征。

1.2 样本量分配方法

在完成样本量测算的基础上，本文进一步讨论样本量在不同类结构特征的分配问题。在大规模问卷调查中，不同调查对象往往具有不同的结构特征（比如，地域、职业类型）。在这种情况下，需要将总体分为几个层次，并按照一定方式（按比例和不按比例）将样本量分配到各个层中，以保证样本能够充分代表总体。其中，分层按比例抽样可以更好地更精确的计算各层的样本量，提高样本的代表性，避免出现简单随机抽样中的集中于某些结构特征或遗漏掉某结构特征。

具体来说，本文以结构特征为标准，将研究对象划分为不同层次，每层按照一定比例分配样本量配额。比如，2015年《中华人民共和国职业分类大典》中职业分类结构共分8个大类、75个中类、434个小类、1481个职业。科技工作者职业共涉及《职业分类大典》中的6个大类、50个中类、183个小类、677个职业，占《职业分类大典》全部职业总数的45.7%[2]。在实现样本量分配时，以科技工作者职业大类为分层标准，将每一大类职业作为一层，将各个大类所包括中类、小类、职业数量在所有中类、小类、职业总量中的占比作为分配比例，对样本量进行分配。假设存在一个标识样本结构特征且结构特征共有I类的变量Vi，i=1,,I。表1给出了以结构特征为分类标准、根据各类结构特征包括一些细化指标（比如中类、小类、职业）（记为Indj，j=1,,J）具体数量（比如，中类数量、小类数量、职业数量）的占比计算分配比例。为方便表述，记属于Vi的细化指标Indj的具体数量为Sij，i=1,,I，j=1,,J，则计算样本分配比例（记为Ri，i=1,,I）的计算公式为：

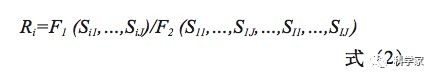
其中，F1和F2表示某一种函数表达式。通过确定F1和F2的具体计算方式，得到样本分配比例。比如，当F1和F2均为求和函数时，属于Vi的样本分配比例为属于第i类结构特征Vi的所有细化指标具体数量之和除以所有结构特征的所有细化指标具体数量之和。

2. 基于总体结构特征的问卷分割设计

2.1 问卷分割方案

问卷分割设计的思想最早由Good提出[3-4]，相关学者在此基础上进行了大量研究[5-10]。假设一份问卷的题目可划分为必答题组和随机题组共2类。其中，必答题组包括背景信息相关题目（记为B）、与研究主题紧密相关或非常重要的题目（记为X），以及代表研究问题或研究目标的响应变量的题目（记为Y，有些问卷不涉及代表响应变量的题目）。随机题目可简单理解为不是所有被调查者都需要回答的题目（记为Z），可等分为K个组（记为Z1，…，ZK）。随机题目的分配需要考虑如下基本原则：反映被调查者同一方面或者相关性很强的题目尽量分配到不同组中。通过这种分配原则，一方面可以增加组间变量的相关性，即便某一组随机题目存在缺失，也可以利用其他组数据与带缺失组数据的相关性进行插补；另一方面可以保证每组题目数量较为均衡，在一定程度上甚至可以帮助确定分组数（即K的取值）。

通常，基于问卷分割技术发放问卷时，需要将样本分为完整样本和缺失样本。即一小部分对总体具有一定代表性的样本回答整个问卷（称为完整样本），其余被调查者只需要回答必答题和一组随机题（称为缺失样本）。结合总体结构特征，无论是完整样本还是缺失样本，都需要覆盖所有结构特征。具体来说，完整样本需要在各类结构特征中都存在一定量的样本，缺失样本同样如此。

假设表2中的问卷共有S个问题，那么理论上，通过问卷分割设计可以将该问卷分成2S-1种不同版本的问卷。显然，这种设计带来过多的问卷版本数量（指数函数增长），在现实中不易操作，很少采用。最简单易行的问卷分割技术是三式设计法[9]。该方法要求在完整版问卷的基础上建立3种形式的问卷，每种形式之间有2/3的条目是重叠的。在调查实施过程中只要求每个参与者回答一种形式问卷。三式设计（或多式设计）是大部分问卷分割设计（有计划缺失设计）的原型，由于问卷中的问题通常存在某几个问题反映被调查者同一方面的组结构，即同一组问题的答案存在较高相关性，因此有研究者关心问卷中的问题的分配方式，如何分配可以使缺失设计带来的信息损失最小。

2.2 缺失数据插补

通过问卷分割设计收集到的数据中存在大量的缺失，这种缺失与通常普遍存在的缺失数据不太相同，主要表现在问卷分割技术的缺失属于有计划的缺失，而不是出于一些敏感、偶然或不可抗力因素，比如受访者对敏感话题的回避、机器故障导致测试数据缺失等等，或者由于个人的主观局限、无意失误或有意隐瞒造成的数据缺失，比如数据收集人员有限时间内未能完成数据收集工作、数据录入人员无意漏录了数据、社会调查中受访者拒绝回答其中的一些问题等等。

众所周知，缺失机制包括完全随机缺失（Missing completely at random，MCAR）、随机缺失（Missing at random，MAR）和非完全随机缺失（Not missing at random，NMAR）[11]。为了方便定义三种缺失机制，令Y=(yij)为数值矩阵，yij表示第i个观测对象、第j个变量yj的取值。定义缺失数据示性矩阵M=(mij)，当mij=1时，yij缺失；当mij=0时，yij不缺失。那么，MCAR表示缺失与数值矩阵Y=(yij)的缺失数据部分和可观测数据部分均无关，即在给定Y的条件下M的条件分布函数与Y无关，f(M|Y)=f(M)。MAR表示缺失仅与数值矩阵Y=(yij)的可观测数据部分有关，即在给定Y的条件下M的条件分布函数与Y中的缺失数据无关，与可观测的数据有关，f(M|Y)=f(M|Yobs)。MNAR表示缺失与数值矩阵Y=(yij)的缺失数据部分和可观测数据部分均有关。问卷分割技术带来的有计划缺失是由已经观测到的数据决定的，不依赖于未观测数据本身，所以符合随机缺失（MAR）机制。

假设调查问卷存在响应变量，即在获得调查数据后需要研究响应变量和某些影响因素（称为自变量）之间的回归关系，那么，问卷分割技术所带来的有计划缺失问题可归纳为因变量随机缺失且自变量完整观测、自变量随机缺失且因变量完整观测和自变量和因变量均存在随机缺失三类：（1）因变量存在随机缺失且自变量完整观测。即因变量随机缺失仅与所有变量的可观测数据部分有关。（2）自变量存在随机缺失且因变量完整观测。即自变量随机缺失仅与所有变量的可观测数据部分有关。（3）自变量和因变量均存在随机缺失。即因变量和自变量随机缺失仅与所有变量的可观测数据部分有关。此外，前文提到的三式设计，所产生的是完全随机缺失数据，使用现代缺失值处理所得参数估计结果是无偏的，其唯一的不足是可能损失统计功效[12]。然而功效的损失与缺失率关系不大，主要取决于变量间预期相关效果量的大小。如果研究假设的相关不强时，在产生3种形式问卷时，各形式问卷之间重叠比例尽量大，同时将预期相关较小的变量应同时放到随机题组中。

面向问卷分割技术带来的缺失数据问题，需要充分考虑不同组随机题目间的相关性，并根据这种相关性获得缺失数据的插补值。因此，有计划缺失数据的插补不是得到缺失数据最好的预测值，而是用合适的值代替缺失值，从不完整观测中挖掘出对推断总体参数有用的信息[13-15]。在不同缺失机制的情况下，缺失数据处理方法通常包括基于完整观测数据部分的处理方法（如完整资料分析法）、加权处理方法（逆概率加权法）、基于插补的处理方法（如热卡插补法）、基于模型的处理方法（如多重插补法）四类[16]。基于完整观测数据部分的处理方法和加权处理方法仅仅用到完整观测的数据，对于问卷分割技术带来的有计划缺失，这两类方法意味着在问卷分割设计时就已决定了缺失样本（只需要回答必答题和一组随机题）无法纳入分析。基于模型的处理方法较为复杂。相比之下，热卡插补法在处理问卷分割调查数据上的优良性质，其基本思想可概括为：依据完整观测和带缺失观测共同观测到的特征，用完整观测对应变量的值来填补带缺失观测上缺失变量的值的插补方法[17]。根据选择完整观测中观测时是否带有随机性，可以分为“随机热卡法”和“确定性热卡法”。“随机热卡法”从完整观测提供的所有可能的插补值中随机选取一个值作为缺失值的代替值，而“确定性热卡法”只选取某个确定的值作为插补值，例如，最近距离热卡法选取完整观测中与带缺失观测最接近的那个观测提供的值。热卡插补法在处理问卷分割调查数据上的优良性质主要表现在：（1）不依赖于任何参数模型；（2）不需要假设数据的分布。因此，热卡插补法对模型和数据分布相对不敏感，不需要研究者准确地估计数据的分布和变量之间的关系，有效避免因模型误设而对参数估计带来的严重偏差。因此，热卡插补法在问卷分割调查数据中更为合适。

但是，热卡插补法需要假定两个观测之间存在一定的相似性。一方面在对随机题进行分组时，将反映被调查者同一方面或者相关性很强的题目尽量分配到不同组中。另一方面，需要选择合适的相似性度量指标，计算不同组题目之间的相似性。实际运用中，主要有以下四种测量指标[1]。

（1）欧氏距离是计算欧式空间中两点之间的距离。欧式距离最大的问题在于它将向量在不同分量上的差异等同看待，这一点有时不能满足实际要求。（2）余弦相似度用两个向量夹角的余弦值来度量两个向量的相似度。余弦相似度度量的是两个向量在n维空间里方向上的接近程度，而对绝对数值不敏感。这一特性对某些数据适用，但对绝对数值有意义的情况就不再适用。（3）马氏距离表示的是数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法，它考虑到各种特性之间的联系并且是独立于测量尺度的。因此，马氏距离有很多优点：马氏距离不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关；由标准化数据和中心化数据计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。但是马氏距离只能用于连续型变量，当数据中含有分类型变量时，马氏距离就不再适用。（4）核函数定义了输入空间到特征空间的一种非线性映射，将向量之间的相似度定义为向量各分量分别计算核函数值的乘积。这种乘积形式的假设虽然忽略了变量之间的相关性，但是是有效的。对于连续型变量，可采用高斯核函数计算题目间相似度。对于分类型变量，可采用Racine和Li提出的核函数，通过用格点法枚举一些取值范围内的值，选择使得模型预测效果最好的宽度参数值[18]。

3. 多水平关系量化方法

3.1 多水平回归关系

多水平回归关系考虑的是量化不同水平下变量间函数关系。之所以需要考虑多水平关系是因为被调查者具有不同的结构特征，换言之，这些被调查者是异质的。在这种情况下，分位回归理论可以刻画数据全貌、处理样本异质性问题、对强影响点稳健且不要求数据分布形式[19]。分位回归的主要模型形式可简单归类为：线性分位回归模型QY(τ│x)=xTβ(τ)和非线性分位回归模型QY(τ│x)=g(x,β(τ))。其中，τ(0,1)表示分位数水平，β(τ)=(β1(τ),,βp(τ)T表示与分位水平τ相关的待估计的分位回归系数。

多水平回归关系的量化即为分位回归参数的估计。本文以线性回归和线性分位回归为例，比较回归参数估计的异同。对于经典的线性回归模型y=β0(τ)+x1β1(τ)++xpβp(τ)+e，一种重要的参数估计方法是最小二乘法。线性回归的参数估计方程可定义为E{(Y-Xβ)2}，那么参数估计问题可表示为=argminβ∑ni=1(yi-xiTβ)2。与线性回归模型参数估计问题类似，分位回归也是寻找使y-Xβ最小的β。但是，分位回归的参数估计主要存在两点不同：（1）表达式并不是取平方，而是借助分位回归特有的损失函数，记为ρτ。其表达式为：ρτ (r)=r{τ-I(r<0)}。其中，I(r<0)为示性函数。（2）参数估计过程是不同分位数水平下各个回归模型参数估计的集合。分位回归的参数估计方程可定义为E{ρτ(Y-Xβ)}。则参数估计问题可表述为：τ=argminβ∑ni=1 ρτ{yi-xiTβ}。

多年来，很多国内外专家一直致力于研究分位回归，将该方法应用于生物统计、经济金融和人文社科等诸多领域。Fox和Rubin研究了损失函数下分位数估计量的可容许性，将平均损失最小作为评价估计优劣的标准之一[20]。Engel根据来自235个欧洲工薪家庭的数据，分析了家庭食物支出和家庭收入间的关系，显示出随着家庭收入水平的提高，食物支出呈现扩散的趋势[21]。Hendricks和Koenker利用分位回归研究了家庭日常用电量与天气特征之间的关系，低分位数曲线反映了基本用电情况，高分位数曲线反映了使用空调所致的用电高峰情况[22]。Bassett和Chen讨论了金融市场中多时期的收益问题[23]。Koenker利用分位回归研究纵向数据，参考经典随机效应估计量的惩罚最小二乘估计解决分位回归模型中的固定效应问题[24]。Wei等人提出了半参数的分位数模型并用它建立生长曲线图，有助于儿医更加有效的追踪儿童的生长发展，大大提高了生长曲线的研究水平[25]。

3.2 多水平结构关系

多水平结构关系是指不同水平下所有变量反映了几个不同维度，而不同维度间又存在着一定关联的情形。有一类常见的多水平结构关系，结构关系中不同维度存在具有层次特征的所属关系，形成树状结构，即一个维度由下一级的某几个维度共同反映，下一级维度又由再下一级的某几个维度共同反映。可见，多水平结构关系本质上研究的是不同水平下可测变量与所反映维度（称为潜变量）间以及不同维度间关系，即结构方程模型。该模型包括测量模型和结构模型两部分[26-27]。对于存在层次特征的结构关系，本质上则通过构建高阶因子模型来实现多水平结构关系的测度问题。最常见的高阶因子模型是二阶因子模型，即一个维度（称为二阶因子）由其他所有维度（都称为一阶因子）共同反映。一阶因子表示的是可测变量共同反映的某个方面，二阶因子是一阶因子的综合体现，反映的是一阶因子共同受到的影响因素。比如，在评价职业满意度及其影响因素时，职业满意度可以作为二阶因子，单位满意度、个人满意度、工作满意度等不同维度可以作为一阶因子，而问卷中具体表现单位满意度、个人满意度、工作满意度方面的题目作为可测变量。

二阶因子模型中测量模型的表达形式如下：

xjh=λjhξj+εjh式（3）

测量模型反映可测变量xjh与一阶因子ξj间的关系。λjh是载荷系数，表示一阶因子ξj对可测变量xjh的影响。εjh为第j个一阶因子ξj中第h个可测变量xjh的测量误差，均值为0，方差为δ2jh，且与一阶因子ξj不相关。

二阶因子模型中结构模型的表达形式如下：

ξj=βjη+δj式（4）

结构模型反映的是一阶因子ξj与二阶因子η间的关系。βj是路径系数，表示二阶因子η对一阶因子ξj的影响。δj为第j个一阶因子ξj的测量误差，均值为0，方差为δj2。

在多水平结构关系的讨论中，二阶因子模型的测量模型和结构模型表达形式都存在一定的变化，多水平二阶因子模型中的测量模型为：xjh=λjh,τξj+εjh,τ。多水平二阶因子模型中的结构模型为：ξj=βi,τη+δj,τ)。其中，τ表示分位数水平。

4. 小结

大规模问卷调查在实际操作过程中总会面临人力、物力和财力投入过多、工期过长等方面的挑战。统计实践表明，长问卷会造成被调查者的回答负担，降低回答率，进而会降低统计调查的数据质量和精度。而且，大规模问卷调查往往涉及具有不同结构特征的调查对象，无论在样本量分配还是数据分析，都需要注意不同结构特征的影响，以保证样本更好地代表总体，实现不同水平下变量间关系的变化。

本文兼顾总体结构特征，从样本量测算与分配方法、问卷分割技术、多水平关系量化方法三个方面探讨大规模问卷调查统计方法，旨在为社会各界和政府等相关部门提供研究思路，具有重大的理论和现实意义。

参考文献

[1] 贾俊平，何晓群，金勇进. 统计学[M]. 中国人民大学出版社，2014.

[2] 周大亚. 我国科技工作者的职业类型及基本特点[J]. 今日科苑，2020(6): 28-30.

[3] Good I J. “Split Questionnaires I,” The American Statistician, 1969, 23 (4), 53-54.

[4] Good I J. “Split Questionnaires II,” The American Statistician, 1970, 24 (2), 36-37.

[5] Adigüzel F, Wedel M. Split questionnaire design for massive surveys[J]. Journal of Marketing Research, 2008, 45(5): 608-617.

[6] Chipperfield J O, Steel D G. Efficiency of split questionnaire surveys[J]. Journal of Statistical Planning and Inference, 2011, 141(5): 1925-1932.

[7] Chipperfield J O, Steel D G. Design and Estimation for Split Questionnaire Surveys[J]. Journal of official statistics, 2009, 25(2):1-31.

[8] Raghunathan T E, Grizzle J E. A split questionnaire survey design[J]. Journal of the American Statistical Association, 1995, 90(429): 54-63.

[9] 赵雪慧. 问卷分割方法在抽样调查中的应用[J]. 兰州商学院学报，2004(1):107-109.

[10] 朱钰，陈晓茹. 问卷分割设计的模拟研究–小域估计的一种应用[J]. 统计与信息论坛，2014，29(10): 14-18.

[11] Little R J A, Rubin D B. Statistical Analysis with Missing Data[M]. New York, Wiley. 1987.

[12] Graham J W, Taylor B J, Olchowski A E, et al. Planned missing data designs in psychological research[J]. Psychological Methods, 2006, 11, 323-343.

[13] Little R J A. Regression with missing X’s: A review[J]. Journal of the American Statistical Association, 1992, 87, 1227-1237.

[14] Robins J M, Rotnitzky A Zhao L P. Estimation of regression coefficients when some regressors are not always observed[J]. Journal of the American Statistical Association, 1994, 89, 846-866.

[15] Tsiatis A A. Semiparametric Theory and Missing Data[M]. Springer Series in Statistics, 2006.

[16] 程豪.逆概率加权多重插补法在我国居民收入影响因素的应用研究[J].统计与信息论坛，2019(7): 26-34.

[17] Reilly M. Data analysis using hot deck multiple imputation[J]. The Statistician, 1993:307-313.

[18] Racine J, LI Q. Nonparametric estimation of regression functions with both categorical and continuous data[J]. Journal of Econometrics, 2004, 119(1): 99-130.

[19] Koenker R. Quantile Regression[M]. Cambridge University Press, 2005.

[20] Fox M, H Rubin. “Admissibility of Quantile Estimates of a Single Location Parameter”[J]. Annals of Mathematical Statistics, 1964, 35, 1019-1030.

[21] Engel E. Die Productions-und Consumtionsver-haltnisse des Konigreichs Sachsen [J].Zeitschrift des Statistischen Bureaus des Koniglich Sachsischen Misisteriums des Innern, 1857, 8, 1-54.

[22] Hendricks W, R Koenker. “Hierarchical Spline Models for Conditional Quantiles and the Demand for Electricity”[J]. Journal of the American Statistical Association, 1991, 87, 58-68.

[23] Bassett G W, Chen H L. Portfolio style: Return-based attribution using quantile regression, 2002, 293-305. In: Fitzenberger B, Koenker R, Machado J A F. (eds) Economic Applications of Quantile Regression. Studies in Empirical Economics. Physica, Heidelberg.

[24] Koenker R. “Quantile Regression for Longitudinal Data”[M]. Journal of Multivariate Analysis, 2004, 91, 74-89.

[25] Wei Y. An Approach to Multivariate Covariate-Dependent Quantile Contours with Application to Bivariate Conditional Growth Charts[J].Journal of the American Statistical Association, 2008 (103), 397-409.

[26] Hair J F, Hult G T M, Ringle C M, et al. A primer on partial least squares structural equation modeling(PLS-SEM)[M]. 2nd Edition. SAGE Publications, Thousand Oaks, 2017.

[27] Lhmller J B. Latent variable path modeling with partial least squares[M]. Physica-Verlag, Heidelberg,1989.

责任编辑：胡林元

封面图片：来源网络

作者简介：

程豪，男，博士，助理研究员，中国科协创新战略研究院，研究方向为指标综合评价、人才工程 评估、复杂数据建模。

网址：研究方法 https://mxgxt.com/news/view/235153

相关内容

竞争对手研究方法
明星研究:维度与方法
竞争对手池的研究方法
《竞争对手研究方法》PPT课件.ppt
竞争对手研究方法模板.ppt
评价节点重要性的几种研究方法.PPT
研究方法｜十分钟弄懂深度访谈（附经典案例）
社交媒体时代网络意见领袖筛选和测量方法研究论文.pdf
网络评论情感可视化技术方法及工具研究*
数据可视化：国内外现状及未来研究方向

随便看看