2.5.2 圆与圆的位置关系

发布时间：2024-12-24 06:09

欢迎到学科网下载资料学习" role="presentation">欢迎到学科网下载资料学习
【基础过关系列】2022-2023 学年高二数学上学期同步知识点剖析精品讲义 (人教 A 版 2019）
跟贵哥学数学，soeasy！" role="presentation">跟贵哥学数学，soeasy！

选择性必修第一册同步巩固，难度 2 颗星！

基础知识

圆与圆的位置关系

1 在同一个平面内，两个不等的圆的位置关系共有五种：外离、外切、相交、内切、内含.
圆心距：两圆圆心的距离叫做圆心距.

2 设两圆 ⊙O1" role="presentation">⊙O1 与圆 ⊙O2" role="presentation">⊙O2 的圆心距为 O1O2=d" role="presentation">O1O2=d，半径分别为 r" role="presentation">r，R(r<R)" role="presentation">R(r<R)，则有

注当两圆相切时分为两种情况：外切和内切.

判断两个圆位置关系的方法

1 几何法
通过判断圆心距与两个圆半径之间的关系从而确定两个圆的位置关系.

2 代数法
设由两圆的方程组成的方程组为 {x2+y2+D1x+E1y+F1=0x2+y2+D2x+E2y+F2=0" role="presentation">{x2+y2+D1x+E1y+F1=0x2+y2+D2x+E2y+F2=0，
由此方程组得：有两组不同的实数解则两圆相交；有两组相同的实数解则两圆相切；无实数解则两圆相离．

【例】判断圆 ⊙O1:x2+y2=1" role="presentation">⊙O1:x2+y2=1 与 ⊙O2:x2+y2−2x−4y+1=0" role="presentation">⊙O2:x2+y2−2x−4y+1=0 的位置关系.
解析几何法
圆 x2+y2=1" role="presentation">x2+y2=1 圆心 O1(0,0)" role="presentation">O1(0,0)，半径 r=1" role="presentation">r=1，
⊙O2:x2+y2−2x−4y+1=0⟹(x−1)2+(y−2)2=4" role="presentation">⊙O2:x2+y2−2x−4y+1=0⟹(x−1)2+(y−2)2=4 圆心 O2(1,2)" role="presentation">O2(1,2)，半径 r=2" role="presentation">r=2，
则圆心距 O1O2=(1−0)2+(2−0)2=5" role="presentation">O1O2=(1−0)2+(2−0)2=5，R−r=3" role="presentation">R−r=3，R−r=1" role="presentation">R−r=1，
则 R−r<O1O2<R−r" role="presentation">R−r<O1O2<R−r，故两个圆相交.
代数法
联立方程 {x2+y2=1x2+y2−2x−4y+1=0" role="presentation">{x2+y2=1x2+y2−2x−4y+1=0 得 5y2−4y=0" role="presentation">5y2−4y=0，显然方程组有两个实数解，
故两个圆相交.

两圆的公共弦方程

(1) 两圆 C1：x2+y2+D1x+E1y+F1=0" role="presentation">C1：x2+y2+D1x+E1y+F1=0， C2：x2+y2+D2x+E2y+F2=0" role="presentation">C2：x2+y2+D2x+E2y+F2=0 相交，交点为 A" role="presentation">A,B" role="presentation">B，
则线段 AB" role="presentation">AB 为两圆的公共弦；

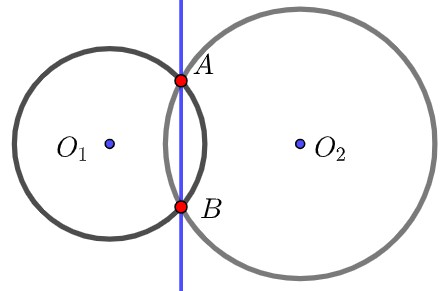
(2) 若两圆 C1：x2+y2+D1x+E1y+F1=0" role="presentation">C1：x2+y2+D1x+E1y+F1=0， C2：x2+y2+D2x+E2y+F2=0" role="presentation">C2：x2+y2+D2x+E2y+F2=0 相交于 A" role="presentation">A,B" role="presentation">B 两点，
则直线 AB" role="presentation">AB 的方程为 (D1−D2)x+(E1−E2)y+F1−F2=0" role="presentation">(D1−D2)x+(E1−E2)y+F1−F2=0.
证明设点 A(x1,y1)" role="presentation">A(x1,y1)，B(x2,y2)" role="presentation">B(x2,y2)，
因为点 A" role="presentation">A 在两圆上，
所以 x12+y12+D1x1+E1y1+F1=0" role="presentation">x12+y12+D1x1+E1y1+F1=0，且 x12+y12+D2x1+E2y1+F2=0" role="presentation">x12+y12+D2x1+E2y1+F2=0，
两等式相减得 (D1−D2)x1+(E1−E2)y1+F1−F2=0(1)" role="presentation">(D1−D2)x1+(E1−E2)y1+F1−F2=0(1)，
同理可得 (D1−D2)x2+(E1−E2)y2+F1−F2=0(2)" role="presentation">(D1−D2)x2+(E1−E2)y2+F1−F2=0(2)，
由 (1)，(2) 可知点 A" role="presentation">A,B" role="presentation">B 均在直线 (D1−D2)x+(E1−E2)y+F1−F2=0" role="presentation">(D1−D2)x+(E1−E2)y+F1−F2=0，
即直线 AB" role="presentation">AB 的方程为 (D1−D2)x+(E1−E2)y+F1−F2=0" role="presentation">(D1−D2)x+(E1−E2)y+F1−F2=0.

【例】若圆 x2+y2=1" role="presentation">x2+y2=1 与 x2+y2+2x−2y=0" role="presentation">x2+y2+2x−2y=0 相交于 A" role="presentation">A，B" role="presentation">B 两点，求直线 AB" role="presentation">AB 的方程.

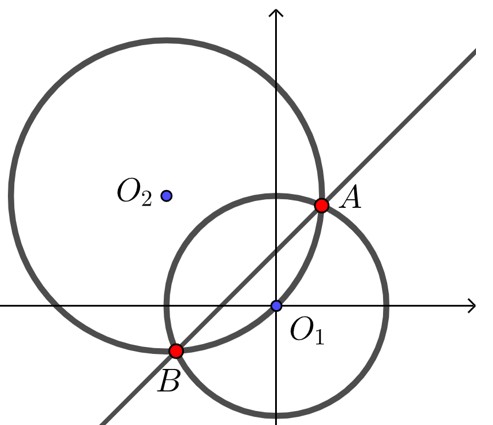
解析两圆相减： x2+y2+2x−2y−(x2+y2)=0−1" role="presentation">x2+y2+2x−2y−(x2+y2)=0−1，化简得 2x−2y+1=0" role="presentation">2x−2y+1=0，
即直线 AB" role="presentation">AB 的方程为 2x−2y+1=0" role="presentation">2x−2y+1=0.

基本方法

【题型1】两圆的位置关系

【典题 1】 已知圆 C1:x2+y2−2ax−2y+a2−15=0" role="presentation">C1:x2+y2−2ax−2y+a2−15=0，圆 C2:x2+y2−4ax−2y+4a2=0(a>0)" role="presentation">C2:x2+y2−4ax−2y+4a2=0(a>0)．试求 a" role="presentation">a 为何值时两圆 C1" role="presentation">C1，C2" role="presentation">C2 的位置关系为：
(1) 相切； " role="presentation"> (2) 相交；" role="presentation"> (3) 外离； " role="presentation"> (4) 内含．
解析圆 C1" role="presentation">C1，C2" role="presentation">C2 的方程，经配方后可得： C1:(x−a)2+(y−1)2=16" role="presentation">C1:(x−a)2+(y−1)2=16，C2:(x−2a)2+(y−1)2=1" role="presentation">C2:(x−2a)2+(y−1)2=1，
∴" role="presentation">∴ 圆心 C1(a,1)" role="presentation">C1(a,1)，C2(2a,1)" role="presentation">C2(2a,1)，半径 r1=4" role="presentation">r1=4，r2=1" role="presentation">r2=1．
∴|C1C2|=(a−2a)2+(1−1)2=a" role="presentation">∴|C1C2|=(a−2a)2+(1−1)2=a．
(1) 当 |C1C2|=r1+r2=5" role="presentation">|C1C2|=r1+r2=5，即 a=5" role="presentation">a=5 时，两圆外切，
当 |C1C2|=r1−r2=3" role="presentation">|C1C2|=r1−r2=3，即 a=3" role="presentation">a=3 时，两圆内切．
(2) 当 3<|C1C2|<5" role="presentation">3<|C1C2|<5，即 3<a<5" role="presentation">3<a<5 时，两圆相交．
(3) 当 |C1C2|>5" role="presentation">|C1C2|>5，即 a>5" role="presentation">a>5 时，两圆外离．
(4) 当 |C1C2|<3" role="presentation">|C1C2|<3，即 a<3" role="presentation">a<3 时，两圆内含．

巩固练习

1. 已知圆 A" role="presentation">A，圆 B" role="presentation">B 相切，圆心距为 10cm" role="presentation">10cm，其中圆 A" role="presentation">A 的半径为 4cm" role="presentation">4cm，则圆 B" role="presentation">B 的半径为 _" role="presentation">_ .

2. 圆 (x+2)2+y2=4" role="presentation">(x+2)2+y2=4 与圆 (x−2)2+(y−1)2=9" role="presentation">(x−2)2+(y−1)2=9 的位置关系为 _" role="presentation">_.

3. 两圆 x2+y2=1" role="presentation">x2+y2=1 和 (x−1)2+(y−a)2=4" role="presentation">(x−1)2+(y−a)2=4 相切，则实数 a" role="presentation">a 的值 _" role="presentation">_．

4. 已知点 O(0,0)" role="presentation">O(0,0),M(1,0)" role="presentation">M(1,0)，且圆 C：(x−5)2+(y−4)2=r2(r>0)" role="presentation">C：(x−5)2+(y−4)2=r2(r>0) 上至少存在一点 P" role="presentation">P，使得 |PO|=2|PM|" role="presentation">|PO|=2|PM|，则 r" role="presentation">r 的最小值是 _" role="presentation">_．

参考答案

答案 6cm" role="presentation">6cm 或 14cm" role="presentation">14cm
解析设圆 B" role="presentation">B 的半径为 rcm" role="presentation">rcm，
因为圆 A" role="presentation">A、圆 B" role="presentation">B 相切，圆心距为 10cm" role="presentation">10cm，
①当圆 A" role="presentation">A 与圆 B" role="presentation">B 外切时，则 r+4=10" role="presentation">r+4=10，解得 r=6" role="presentation">r=6；
②当圆 A" role="presentation">A 与圆 B" role="presentation">B 内切时，则 |r−4|=10" role="presentation">|r−4|=10，解得 r=14" role="presentation">r=14．
故圆 B 半径为 6cm" role="presentation">6cm 或 14cm" role="presentation">14cm. 答案相交
解析圆 (x+2)2+y2=4" role="presentation">(x+2)2+y2=4 的圆心 C1(−2，0)" role="presentation">C1(−2，0)，半径 r=2" role="presentation">r=2．
圆 (x−2)2+(y−1)2=9" role="presentation">(x−2)2+(y−1)2=9 的圆心 C2(2，1)" role="presentation">C2(2，1)，半径 R=3" role="presentation">R=3，
两圆的圆心距离 d=(−2−2)2+(0−1)2=17" role="presentation">d=(−2−2)2+(0−1)2=17，
R+r=5" role="presentation">R+r=5，R−r=1" role="presentation">R−r=1，R+r>d>R−r" role="presentation">R+r>d>R−r，
所以两圆相交．答案 a=±22" role="presentation">a=±22 或 a=0" role="presentation">a=0
解析两圆圆心距为 a2+1" role="presentation">a2+1，因为两圆相切，
所以 a2+1=2+1" role="presentation">a2+1=2+1 或 a2+1=2−1" role="presentation">a2+1=2−1，
即 a2+1=3" role="presentation">a2+1=3 或 a2+1=1" role="presentation">a2+1=1．所以 a=±22" role="presentation">a=±22 或 a=0" role="presentation">a=0．答案 5−2" role="presentation">5−2
解析设 P(x,y)" role="presentation">P(x,y)，
∵|PO|=2|PM|" role="presentation">∵|PO|=2|PM|，
∴x2+y2=2(x−1)2+2y2" role="presentation">∴x2+y2=2(x−1)2+2y2，即 (x−2)2+y2=2" role="presentation">(x−2)2+y2=2，
圆心距 =(5−2)2+(4−0)2=r+2" role="presentation">=(5−2)2+(4−0)2=r+2，
∴r" role="presentation">∴r 的最小值是 5−2" role="presentation">5−2．

【题型2】两圆公共弦问题

【典题 1】 已知圆 C1:x2+y2+6x−4=0" role="presentation">C1:x2+y2+6x−4=0 和圆 C2:x2+y2+6y−28=0" role="presentation">C2:x2+y2+6y−28=0．
(1) 求两圆公共弦所在直线的方程；
(2) 求经过两圆交点且圆心在直线 x−y−4=0" role="presentation">x−y−4=0 上的圆的方程．
解析 (1) 设两圆交点为 A(x1,y1)" role="presentation">A(x1,y1),B(x2,y2)" role="presentation">B(x2,y2)，
则 A" role="presentation">A,B" role="presentation">B 两点坐标是方程组 {x2+y2+6x−4=0(1)x2+y2+6y−28=0(2)" role="presentation">{x2+y2+6x−4=0(1)x2+y2+6y−28=0(2) 的解．
①－" role="presentation">－②得 x−y+4=0" role="presentation">x−y+4=0．
∵A,B" role="presentation">∵A,B 两点坐标都满足此方程，
∴x−y+4=0" role="presentation">∴x−y+4=0 即为两圆公共弦所在直线的方程．
(2) 方法一：解方程组 {x2+y2+6x−4=0x2+y2+6y−28=0" role="presentation">{x2+y2+6x−4=0x2+y2+6y−28=0 两圆的交点 A(−1,3)" role="presentation">A(−1,3)，B(−6,−2)" role="presentation">B(−6,−2)．
设所求圆的圆心为 (a,b)" role="presentation">(a,b)，因圆心在直线 x−y−4=0" role="presentation">x−y−4=0 上，
故 b=a－4" role="presentation">b=a－4．
则 (a+1)2+(a−4−3)2=(a+6)2+(a−4+2)2" role="presentation">(a+1)2+(a−4−3)2=(a+6)2+(a−4+2)2，解得 a=12" role="presentation">a=12，
故圆心为 (12,−72)" role="presentation">(12,−72)，半径为 892" role="presentation">892．
故圆的方程为 (x−12)2+(y+72)2=892" role="presentation">(x−12)2+(y+72)2=892，
即 x2+y2−x+7y−32=0" role="presentation">x2+y2−x+7y−32=0．
方法二：设所求圆的方程为 x2+y2+6x−4+λ(x2+y2+6y−28)=0(λ≠−1)" role="presentation">x2+y2+6x−4+λ(x2+y2+6y−28)=0(λ≠−1)，
其圆心为 (−31+λ,−3λ1+λ)" role="presentation">(−31+λ,−3λ1+λ)，代入 x−y−4=0" role="presentation">x−y−4=0，解得 λ=−7" role="presentation">λ=−7．
故所求圆的方程为 x2+y2−x+7y−32=0" role="presentation">x2+y2−x+7y−32=0．
点拨过两圆 C1：x2+y2+D1x+E1y+F1=0" role="presentation">C1：x2+y2+D1x+E1y+F1=0， C2：x2+y2+D2x+E2y+F2=0" role="presentation">C2：x2+y2+D2x+E2y+F2=0 交点的圆系方程为 x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0" role="presentation">x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0
(λ≠−1" role="presentation">λ≠−1, 此圆系不含 C2：x2+y2+D2x+E2y+F2=0" role="presentation">C2：x2+y2+D2x+E2y+F2=0)
特别地，当 λ=−1" role="presentation">λ=−1 时，上述方程为一次方程.
两圆相交时，表示公共弦方程；两圆相切时，表示公切线方程.

巩固练习

1.(多选) 已知圆 C1：x2+y2=1" role="presentation">C1：x2+y2=1，圆 C2：(x−3)2+(y+4)2=r2(r>0)" role="presentation">C2：(x−3)2+(y+4)2=r2(r>0)，则 (　　)
A．若圆 C1" role="presentation">C1 与圆 C2" role="presentation">C2 无公共点，则 0<r<4" role="presentation">0<r<4
B．当 r=5" role="presentation">r=5 时，两圆公共弦长所在直线方程为 6x−8y−1=0" role="presentation">6x−8y−1=0
C．当 r=2" role="presentation">r=2 时，P" role="presentation">P、Q" role="presentation">Q 分别是圆 C1" role="presentation">C1 与圆 C2" role="presentation">C2 上的点，则 |PQ|" role="presentation">|PQ| 的取值范围为 [2,8]" role="presentation">[2,8]
D．当 0<r<4" role="presentation">0<r<4 时，过直线 6x−8y+r2－26=0" role="presentation">6x−8y+r2－26=0 上任意一点分别作圆 C1" role="presentation">C1、圆 C2" role="presentation">C2 切线，则切线长相等

2. 圆 x2+y2−2x−5=0" role="presentation">x2+y2−2x−5=0 和圆 x2+y2+2x−4y−4=0" role="presentation">x2+y2+2x−4y−4=0 的交点为 A" role="presentation">A，B" role="presentation">B，则线段 AB" role="presentation">AB 的垂直平分线的方程为 _" role="presentation">_．

3. 如图所示，在圆 O" role="presentation">O 上任取 C" role="presentation">C 点为圆心，作一圆 C" role="presentation">C 与圆 O" role="presentation">O 的直径 AB" role="presentation">AB 相切于 D" role="presentation">D，圆 C" role="presentation">C 与圆 O" role="presentation">O 交于 E" role="presentation">E，F" role="presentation">F，且 EF" role="presentation">EF 与 CD" role="presentation">CD 相交于 H" role="presentation">H．

求证：EF" role="presentation">EF 平分 CD" role="presentation">CD．

参考答案

答案 BCD" role="presentation">BCD
解析圆 C1：x2+y2=1" role="presentation">C1：x2+y2=1，其圆心为 (0,0)" role="presentation">(0,0)，半径为 1" role="presentation">1，
圆 C2：(x－3)2+(y+4)2=r2(r>0)" role="presentation">C2：(x－3)2+(y+4)2=r2(r>0)，其圆心为 (3,4)" role="presentation">(3,4)，半径为 r" role="presentation">r．
对于 A" role="presentation">A，两圆的圆心距 |C1C2|=9+16=5" role="presentation">|C1C2|=9+16=5，
若圆 C1" role="presentation">C1 与圆 C2" role="presentation">C2 无公共点，即两圆内含或外离，
必有 r+1<5" role="presentation">r+1<5 或 r−1>5" role="presentation">r−1>5，即 0<r<4" role="presentation">0<r<4 或 r>6" role="presentation">r>6，故 A" role="presentation">A 错误；
对于 B" role="presentation">B，当 r=5" role="presentation">r=5 时，圆 C2：(x−3)2+(y+4)2=25" role="presentation">C2：(x−3)2+(y+4)2=25，
联立圆 C1" role="presentation">C1 和圆 C2" role="presentation">C2 的方程可得 6x−8y−1=0" role="presentation">6x−8y−1=0，
即两圆公共弦长所在直线方程为 6x−8y−1=0" role="presentation">6x−8y−1=0，B" role="presentation">B 正确；
对于 C" role="presentation">C，当 r=2" role="presentation">r=2 时，圆 C2：（x−3）2+(y+4)2=r2" role="presentation">C2：（x−3）2+(y+4)2=r2，
P" role="presentation">P、Q" role="presentation">Q 分别是圆 C1" role="presentation">C1 与圆 C2" role="presentation">C2 上的点，
则 |PQ|" role="presentation">|PQ| 的最小值为 |C1C2|−2−1=2" role="presentation">|C1C2|−2−1=2，最大值为 |C1C2|+2+1=8" role="presentation">|C1C2|+2+1=8，
即 |PQ|" role="presentation">|PQ| 的取值范围为 [2,8]" role="presentation">[2,8]，故 C" role="presentation">C 正确；
对于 D" role="presentation">D，当 0<r<4" role="presentation">0<r<4 时，两圆外离，
过 P(x0,y0)" role="presentation">P(x0,y0) 引两圆 C1" role="presentation">C1，C2" role="presentation">C2 的切线分别为 PA" role="presentation">PA，PB" role="presentation">PB，
由 |PA|=|PB|" role="presentation">|PA|=|PB|，得 |PC1|2−1=|PC2|2−r2" role="presentation">|PC1|2−1=|PC2|2−r2，
即 x02+y02−1=(x0−3)2+(y0+4)2−r2" role="presentation">x02+y02−1=(x0−3)2+(y0+4)2−r2，
整理得： 6x0−8y0+r2−26=0，" role="presentation">6x0−8y0+r2−26=0，，
可得过直线 6x－8y+r2－26=0" role="presentation">6x－8y+r2－26=0 上任意一点分别作圆 C1" role="presentation">C1、圆 C2" role="presentation">C2 切线，则切线长相等，
故 D" role="presentation">D 正确．
故选：BCD" role="presentation">BCD．

答案 x+y−1=0" role="presentation">x+y−1=0
解析 ∵" role="presentation">∵ 圆 x2+y2−2x−5=0" role="presentation">x2+y2−2x−5=0 的圆心 M(1,0)" role="presentation">M(1,0)，
圆 x2+y2+2x−4y−4=0" role="presentation">x2+y2+2x−4y−4=0 的圆心 N(−1,2)" role="presentation">N(−1,2)，
又 ∵" role="presentation">∵ 圆 x2+y2−2x−5=0" role="presentation">x2+y2−2x−5=0 和圆 x2+y2+2x−4y−4=0" role="presentation">x2+y2+2x−4y−4=0 的交点为 A" role="presentation">A，B" role="presentation">B，
∴" role="presentation">∴ 线段 AB" role="presentation">AB 的垂直平分线是 MN" role="presentation">MN 所在的直线，
∴MN" role="presentation">∴MN 的方程为： y−02−0=x−1−1−1" role="presentation">y−02−0=x−1−1−1，即 x+y−1=0" role="presentation">x+y−1=0．

证明以 AB" role="presentation">AB 所在直线为 x" role="presentation">x 轴，O" role="presentation">O 为坐标原点建立平面直角坐标系．

如图，设 |AB|=2r" role="presentation">|AB|=2r，D(a,0)" role="presentation">D(a,0)，
则 |CD|=r2−a2" role="presentation">|CD|=r2−a2， ∴C(a,r2−a2)" role="presentation">∴C(a,r2−a2)．
∴" role="presentation">∴ 圆 O:x2+y2=r2" role="presentation">O:x2+y2=r2，圆 C:(x−a)2+(y−r2−a2)2=r2−a2" role="presentation">C:(x−a)2+(y−r2−a2)2=r2−a2．
两方程作差得直线 EF" role="presentation">EF 的方程为 2ax+2r2−a2y=r2+a2" role="presentation">2ax+2r2−a2y=r2+a2．
令 x=a" role="presentation">x=a，得 y=12r2−a2" role="presentation">y=12r2−a2，
∴H(a,12r2−a2)" role="presentation">∴H(a,12r2−a2)，即 H" role="presentation">H 为 CD" role="presentation">CD 的中点．
∴EF" role="presentation">∴EF 平分 CD" role="presentation">CD．

分层练习

【A组---基础题】

1. 圆 O1:x2+y2=2" role="presentation">O1:x2+y2=2 和圆 O2:x2+y2+4y+3=0" role="presentation">O2:x2+y2+4y+3=0 的位置关系是 (　　)
A．相离 " role="presentation"> B．外切 " role="presentation"> C．内切 " role="presentation">D．相交

2. 设 r>0" role="presentation">r>0，两圆 (x−1)2+(y+3)2=r2" role="presentation">(x−1)2+(y+3)2=r2 与 x2+y2=16" role="presentation">x2+y2=16 的位置关系不可能是 (　　)
A．相切 " role="presentation"> B．相交 " role="presentation"> C．内切和内含 " role="presentation"> D．外切和外离

3.(多选) 点 P" role="presentation">P 在圆 C1：x2+y2=1" role="presentation">C1：x2+y2=1 上，点 Q" role="presentation">Q 在圆 C2：x2+y2－6x+8y+24=0" role="presentation">C2：x2+y2－6x+8y+24=0 上，则 (　　)
A．|PQ|" role="presentation">|PQ| 的最小值为 0" role="presentation">0
B．|PQ|" role="presentation">|PQ| 的最大值为 7" role="presentation">7
C．两个圆心所在的直线斜率为 −43" role="presentation">−43
D．两个圆相交弦所在直线的方程为 6x－8y－25=0" role="presentation">6x－8y－25=0

4. 圆 C1:x2+y2+4x−4y−5=0" role="presentation">C1:x2+y2+4x−4y−5=0，圆 C2:x2+y2−8x+4y+7=0" role="presentation">C2:x2+y2−8x+4y+7=0 的公切线条数是 _" role="presentation">_．

5. 以 (3，−4)" role="presentation">(3，−4) 为圆心，且与圆 x2+y2=64" role="presentation">x2+y2=64 内切的圆的方程是 _" role="presentation">_．

6. 已知点 A(−1,0)" role="presentation">A(−1,0),B(1,2)" role="presentation">B(1,2)，圆 C：(x−a)2+y2=25(a>0)" role="presentation">C：(x−a)2+y2=25(a>0) 上存在唯一的点 P" role="presentation">P，使 PA2+PB2=12" role="presentation">PA2+PB2=12，则实数 a" role="presentation">a 的值是 _" role="presentation">_．

7. 半径为 3" role="presentation">3 的圆与 x" role="presentation">x 轴相切，且与圆 x2+(y−1)2=1" role="presentation">x2+(y−1)2=1 外切，求此圆的方程．

8. 求与圆 C:x2+y2−2x=0" role="presentation">C:x2+y2−2x=0 外切且与直线 l:x+3y=0" role="presentation">l:x+3y=0 相切于点 M(3,−3)" role="presentation">M(3,−3) 的圆的方程．

9. 已知圆 C1:x2+y2+2x−6y+1=0" role="presentation">C1:x2+y2+2x−6y+1=0，圆 C2:x2+y2−4x+2y−11=0" role="presentation">C2:x2+y2−4x+2y−11=0．求两圆的公共弦所在直线的方程及公共弦长．

参考答案

答案 D" role="presentation">D
解析圆 x2+y2=2" role="presentation">x2+y2=2 的圆心 (0，0)" role="presentation">(0，0)，半径为 R=2" role="presentation">R=2，
圆 x2+y2+4y+3=0" role="presentation">x2+y2+4y+3=0 化为标准方程得： x2+(y+2)2=1" role="presentation">x2+(y+2)2=1，
故圆心坐标 (0，−2)" role="presentation">(0，−2)，半径为 r=1" role="presentation">r=1，
∵" role="presentation">∵ 圆心之间的距离 d=2" role="presentation">d=2，R+r=1+2>2" role="presentation">R+r=1+2>2，R−r=2−1<2" role="presentation">R−r=2−1<2
∴R−r<d<R+r" role="presentation">∴R−r<d<R+r，
则两圆的位置关系是相交．
故选：D" role="presentation">D．

答案 D" role="presentation">D
解析圆 (x−1)2+(y+3)2=r2" role="presentation">(x−1)2+(y+3)2=r2 与 x2+y2=16" role="presentation">x2+y2=16，
所以两圆的圆心分别为 (1,−3)" role="presentation">(1,−3)，(0,0)" role="presentation">(0,0)，半径分别为 r" role="presentation">r，4" role="presentation">4，
则两圆的圆心距为 (1−0)2+(−3−0)2=10" role="presentation">(1−0)2+(−3−0)2=10，
因为 r＞0" role="presentation">r＞0，
所以 r+4>10" role="presentation">r+4>10，
则两圆不可能是外切和相离．
故选：D" role="presentation">D．

答案 BC" role="presentation">BC
解析根据题意，圆 C1：x2+y2=1" role="presentation">C1：x2+y2=1，其圆心 C1(0,0)" role="presentation">C1(0,0)，半径 R=1" role="presentation">R=1，
圆 C2：x2+y2－6x+8y+24=0" role="presentation">C2：x2+y2－6x+8y+24=0，其圆心 C2(3,－4)" role="presentation">C2(3,－4)，半径 r=1" role="presentation">r=1，
圆心距 |C1C2|=16+9=5" role="presentation">|C1C2|=16+9=5，
则 |PO|" role="presentation">|PO| 的最小值为 |C1C2|−R−r=3" role="presentation">|C1C2|−R−r=3，最大值为 |C1C2|+R+r=7" role="presentation">|C1C2|+R+r=7，
故 A" role="presentation">A 错误，B" role="presentation">B 正确；
对于 C" role="presentation">C，圆心 C1(0,0)" role="presentation">C1(0,0)，圆心 C2(3,−4)" role="presentation">C2(3,−4)，
则两个圆心所在的直线斜率 k=−4−03−0=−43" role="presentation">k=−4−03−0=−43，C" role="presentation">C 错误，
对于 D" role="presentation">D，两圆圆心距 |C1C2|=5" role="presentation">|C1C2|=5，有 |C1C2|>R+r=2" role="presentation">|C1C2|>R+r=2，
两圆外切，不存在公共弦，D" role="presentation">D 错误．
故选：BC" role="presentation">BC．

答案 3" role="presentation">3
解析圆 C1:(x+2)2+(y−2)2=13" role="presentation">C1:(x+2)2+(y−2)2=13，圆 C2:(x−4)2+(y+2)2=13" role="presentation">C2:(x−4)2+(y+2)2=13，
因此两圆的圆心坐标分别为 C1(−2,2)" role="presentation">C1(−2,2)，C2(4,−2)" role="presentation">C2(4,−2)，两圆的半径 r1=r2=13" role="presentation">r1=r2=13．
圆心距 |C1C2|=(−2−4)2+(2+2)2=213=r1+r2" role="presentation">|C1C2|=(−2−4)2+(2+2)2=213=r1+r2，
∴" role="presentation">∴ 两圆外切，有 3" role="presentation">3 条公切线．

答案 (x−3)2+(y+4)2=9" role="presentation">(x−3)2+(y+4)2=9 或 (x−3)2+(y+4)2=169" role="presentation">(x−3)2+(y+4)2=169
解析设所求的圆的方程为 (x−3)2+(y+4)2=r2，r>0" role="presentation">(x−3)2+(y+4)2=r2，r>0，
则由题意可得 9+16=|8−r|" role="presentation">9+16=|8−r|，求得 r=3" role="presentation">r=3，或 r=13" role="presentation">r=13，
故所求的圆的方程为 (x−3)2+(y+4)2=9" role="presentation">(x−3)2+(y+4)2=9 或 (x−3)2+(y+4)2=169" role="presentation">(x−3)2+(y+4)2=169，
故答案为： (x−3)2+(y+4)2=9" role="presentation">(x−3)2+(y+4)2=9 或 (x−3)2+(y+4)2=169" role="presentation">(x−3)2+(y+4)2=169.

答案 ±43" role="presentation">±43 或 ±22" role="presentation">±22
解析设 P(x,y)" role="presentation">P(x,y)，则 PA2=(x+1)2+(y−0)2=x2+y2+2x+1" role="presentation">PA2=(x+1)2+(y−0)2=x2+y2+2x+1，
PB2=(x−1)2+(y−2)2=x2+y2−2x−4y+5" role="presentation">PB2=(x−1)2+(y−2)2=x2+y2−2x−4y+5，
∵PA2+PB2=12" role="presentation">∵PA2+PB2=12，
∴x2+y2−2y－3=0" role="presentation">∴x2+y2−2y－3=0，即 x2+(y−1)2=4" role="presentation">x2+(y−1)2=4；
∴P" role="presentation">∴P 点轨迹方程为 x2+(y−1)2=4" role="presentation">x2+(y−1)2=4．
又圆 C" role="presentation">C 上存在唯一的点 P 符合题意，
∴" role="presentation">∴ 两圆相切，
∴a2+1=7" role="presentation">∴a2+1=7 或 a2+1=3" role="presentation">a2+1=3，解得 a=±43" role="presentation">a=±43 或 a=±22" role="presentation">a=±22，
∴" role="presentation">∴ 实数 a" role="presentation">a 的值为 ±43" role="presentation">±43 或 ±22" role="presentation">±22．

答案 (x±23)2+(y−3)2=9" role="presentation">(x±23)2+(y−3)2=9 或 x2+(y+3)2=9" role="presentation">x2+(y+3)2=9
解析因为所求圆的半径为 3" role="presentation">3 且与 x" role="presentation">x 轴相切，
所以设圆心坐标为 (a,－3)" role="presentation">(a,－3) 或 (a,3)" role="presentation">(a,3)．
又因为所求圆与圆 x2+(y−1)2=1" role="presentation">x2+(y−1)2=1 外切，
所以 a2+4=4" role="presentation">a2+4=4 或 a2+16=4" role="presentation">a2+16=4，即 a=±23" role="presentation">a=±23 或 a=0" role="presentation">a=0．
所以所求圆的方程为 (x±23)2+(y−3)2=9" role="presentation">(x±23)2+(y−3)2=9 或 x2+(y+3)2=9" role="presentation">x2+(y+3)2=9．

答案 (x−4)2+y2=4" role="presentation">(x−4)2+y2=4
解析圆 C" role="presentation">C 的方程可化为 (x−1)2+y2=1" role="presentation">(x−1)2+y2=1，圆心 C(1,0)" role="presentation">C(1,0)，半径为 1" role="presentation">1．
设所求圆的方程为 (x−a)2+(y−b)2=r2(r>0)" role="presentation">(x−a)2+(y−b)2=r2(r>0)，
由题意可得 {(a−1)2+b2=r+1b+3a−3×(−33)=−1|a+3b|2=r" role="presentation">{(a−1)2+b2=r+1b+3a−3×(−33)=−1|a+3b|2=r，解得 {a=4b=0r=2" role="presentation">{a=4b=0r=2，
所以所求圆的方程为 (x−4)2+y2=4" role="presentation">(x−4)2+y2=4．

答案 245" role="presentation">245
解析联立方程组 {x2+y2+2x−6y+1=0(1)x2+y2−4x+2y−11=0(2)" role="presentation">{x2+y2+2x−6y+1=0(1)x2+y2−4x+2y−11=0(2)
①－②得 3x−4y+6=0" role="presentation">3x−4y+6=0．
∴3x−4y+6=0" role="presentation">∴3x−4y+6=0 即为两圆公共弦所在直线的方程．
易知圆 C1" role="presentation">C1 的圆心 (−1,3)" role="presentation">(−1,3)，半径 r=3" role="presentation">r=3．
又 C1" role="presentation">C1 到直线 AB" role="presentation">AB 的距离为 d=|−1×3−4×3+6|32+42=95" role="presentation">d=|−1×3−4×3+6|32+42=95，
∴|AB|=2r2−d2=232−(95)2=245" role="presentation">∴|AB|=2r2−d2=232−(95)2=245，
即两圆的公共弦长为 245" role="presentation">245．

【B组---提高题】

1.(多选) 已知点 Q(4,0)" role="presentation">Q(4,0)，过圆 (x−4)2+y2=16" role="presentation">(x−4)2+y2=16 上的一动点 P" role="presentation">P 作圆 (x−4)2+y2=4" role="presentation">(x−4)2+y2=4 的两条切线 PA" role="presentation">PA、PB" role="presentation">PB，切点分别为 A" role="presentation">A、B" role="presentation">B，两个切点 A" role="presentation">A、B" role="presentation">B 之间的线段 AB" role="presentation">AB 称为切点弦．则下列结论正确的是 (　　)
A．PQ⊥AB" role="presentation">PQ⊥AB " role="presentation"> B． |PA|=23" role="presentation">|PA|=23 " role="presentation"> C．|AB|=3" role="presentation">|AB|=3" role="presentation"> D．四边形 APBQ" role="presentation">APBQ 的面积为 43" role="presentation">43

2. 如图，设圆 C1：(x−5)2+(y+2)2=4" role="presentation">C1：(x−5)2+(y+2)2=4，圆 C2：(x−7)2+(y+1)2=25" role="presentation">C2：(x−7)2+(y+1)2=25，点 A" role="presentation">A、B" role="presentation">B 分别是圆 C1" role="presentation">C1，C2" role="presentation">C2 上的动点，P" role="presentation">P 为直线 y=x" role="presentation">y=x 上的动点，则 |PA|+|PB|" role="presentation">|PA|+|PB| 的最小值为 _" role="presentation">_ .

参考答案

答案 ABD" role="presentation">ABD
解析因为 Q(4,0)" role="presentation">Q(4,0) 为两已知圆的圆心，由几何性质可知 |PA|=|PB|" role="presentation">|PA|=|PB|，|QA|=|QB|" role="presentation">|QA|=|QB|，
所以 PQ⊥AB" role="presentation">PQ⊥AB，故 A" role="presentation">A 正确；
因为 |PQ|=4" role="presentation">|PQ|=4，|AQ|=|BQ|=2" role="presentation">|AQ|=|BQ|=2，
所以 |PB|=|PA|=|QP|2−|QA|2=23" role="presentation">|PB|=|PA|=|QP|2−|QA|2=23，故 B" role="presentation">B 正确；
因为 sin⁡∠APQ=|AQ||PQ|=12" role="presentation">sin⁡∠APQ=|AQ||PQ|=12，
又 ∠APQ" role="presentation">∠APQ 为锐角，所以 ∠APQ=30°" role="presentation">∠APQ=30°，同理可得 ∠BPQ=30°" role="presentation">∠BPQ=30°，
所以 ∠APB=60°" role="presentation">∠APB=60°，则 △APB" role="presentation">△APB 为等边三角形，所以 |AB|=23" role="presentation">|AB|=23，
S△APBQ=2S△APQ=|PA|⋅|AQ|=43" role="presentation">S△APBQ=2S△APQ=|PA|⋅|AQ|=43，故 C" role="presentation">C 错误，D" role="presentation">D 正确，
故选：ABD" role="presentation">ABD．答案 313−7" role="presentation">313−7
解析依题意可知圆 C1" role="presentation">C1 的圆心 (5,－2)" role="presentation">(5,－2)，r=2" role="presentation">r=2，圆 C2" role="presentation">C2 的圆心 (7,－1)" role="presentation">(7,－1)，R=5" role="presentation">R=5，如图所示：

对于直线 y=x" role="presentation">y=x 上的任一点 P" role="presentation">P，由图象可知，要使 |PA|+|PB|" role="presentation">|PA|+|PB| 的得最小值，
则问题可转化为求 |PC1|+|PC2|－R－r=|PC1|+|PC2|－7" role="presentation">|PC1|+|PC2|－R－r=|PC1|+|PC2|－7 的最小值，
即可看作直线 y=x" role="presentation">y=x 上一点到两定点距离之和的最小值减去 7" role="presentation">7，
由平面几何的知识易知当 C1" role="presentation">C1 关于直线 y=x" role="presentation">y=x 对称的点为 C1′(－2,5)" role="presentation">C1′(－2,5)，
与 P" role="presentation">P、C2" role="presentation">C2 共线时，|PC1|+|PC2|" role="presentation">|PC1|+|PC2| 的最小值，
取得最小值，即直线 y=x" role="presentation">y=x 上一点到两定点距离之和取得最小值为 |CC2|=313" role="presentation">|CC2|=313，
∴|PA|+|PB|" role="presentation">∴|PA|+|PB| 的最小值 [=|PC1|+|PC2|−7=313−7" role="presentation">[=|PC1|+|PC2|−7=313−7．

【C组---拓展题】

1. 两圆 x2+y2+2ax+2ay+2a2−1=0" role="presentation">x2+y2+2ax+2ay+2a2−1=0 和 x2+y2+2bx+2by+2b2−2=0" role="presentation">x2+y2+2bx+2by+2b2−2=0 的公共弦中，最长的弦等于 _" role="presentation">_．

参考答案

答案 2" role="presentation">2
解析将两圆方程相减得公共弦所在直线方程： (2a−2b)x+(2a−2b)y+2a2−2b2+1=0" role="presentation">(2a−2b)x+(2a−2b)y+2a2−2b2+1=0，
x2+y2+2ax+2ay+2a2−1=0" role="presentation">x2+y2+2ax+2ay+2a2−1=0 化为标准方程为 (x+a)2+(y+a)2=1" role="presentation">(x+a)2+(y+a)2=1，
其圆心为 (−a,−a)" role="presentation">(−a,−a)，半径为 1" role="presentation">1，
圆心到公共弦所在直线的距离为 d=|(2a−2b)(−a)×2+2a2−2b2+1|22|a−b|=|1−2(a−b)2|22|a−b|" role="presentation">d=|(2a−2b)(−a)×2+2a2−2b2+1|22|a−b|=|1−2(a−b)2|22|a−b|
所以公共弦长为 21−d2=21−(1−2(a−b)222|a−b|)2" role="presentation">21−d2=21−(1−2(a−b)222|a−b|)2=21−((a−b)22+18(a−b)2−12)" role="presentation">=21−((a−b)22+18(a−b)2−12)
≤21−(2116−12)=2" role="presentation">≤21−(2116−12)=2，
故答案为：2" role="presentation">2.

网址：2.5.2 圆与圆的位置关系 https://mxgxt.com/news/view/457244

上一篇: “他经济”下，探寻男性情感内容蓝

下一篇: 这回，“一夜涨粉300万”的大圆

2.5.2 圆与圆的位置关系

基础知识

圆与圆的位置关系

判断两个圆位置关系的方法

两圆的公共弦方程

基本方法

【题型1】两圆的位置关系

巩固练习

【题型2】两圆公共弦问题

巩固练习

分层练习

【A组---基础题】

【B组---提高题】

【C组---拓展题】

相关内容

随便看看

最新实时动态

热点实时动态

专题

推荐实时动态