杨振宁教授漫谈:数学和物理的关系
原文出自:张奠宙《和杨振宁教授漫谈:数学和物理的关系》,首发于“超级数学建模”公号。

杨振宁是当代的大物理学家, 又是现代数学发展的重要推动者, 他的两项巨大成就: 杨–密尔斯规范场和杨–巴克斯特方程, 成为80年代以来一系列数学研究的出发点, 其影响遍及微分几何、偏微分方程、低维拓扑、辫结理论、量子群等重大数学学科。笔者曾在「杨振宁与当代数学」的访谈录中有过较为详细的介绍(此文的中文版在台湾「数学传播」1992年4月发表, 内容不全相同的英文版刊于「Mathematical Intelligencer」Vol.15,NO.4,1993。它的中译文已被收入杨振宁的新着「读书教学再十年」(台湾时报出版公司,1995), 这里记录的有关数学与物理学的关系, 来自笔者在1995年末在纽约州立大学(石溪) 访问杨振宁先生时的一些谈话材料, 因为不是系统的谈话, 故称「漫谈」。

一、有关数学的两则「笑话」
1980年代初, 杨振宁曾在韩国汉城作物理学演讲时说「有那么两种数学书: 第一种你看了第一页就不想看了, 第二种是你看了第一句话就不想看了」。当时引得物理学家们轰堂大笑。此话事出有因。1969年, 杨振宁察觉物理上的规范场理论和数学上的纤维丛理论可能有关系, 就把著名拓扑学家Steenrod着的「The Topology of Fibre Bundles纤维丛的拓扑)」一书拿来读, 结果是一无所获。原因是该书从头至尾都是定义、定理、推论式的纯粹抽象演绎, 生动活泼的实际背景淹没在形式逻辑的海洋之中, 使人摸不着头脑。
上述汉城演讲中那句话本来是即兴所开的玩笑, 不能当真的。岂料不久之后被「Mathematical Intelligencer」捅了出来, 公之与众。在数学界当然会有人表示反对, 认为数学书本来就应该是那样的。不过, 杨振宁先生说「我相信会有许多数学家支持我, 因为数学毕竟要让更多的人来欣赏, 才会产生更大的效果」。
我想, 杨振宁是当代物理学家中特别偏爱数学, 而且大量运用数学的少数物理学者之一。如果连他也对某些数学著作的表达方式啧有烦言, 遑论其它的物理学家? 更不要说生物学家、经济学家、一般的社会科学家和读者了。
另一则笑话, 可在波兰裔美国数学名家S.M.Ulam 的自传「一个数学家的遭遇(Advantures of a mathematician) 」中读到。该书294页上写道: 「杨振宁, 诺贝尔物理学奖获得者, 讲了一个有关现时数学家和物理家间不同思考方式的故事: 一天晚上, 一帮人来到一个小镇。他们有许多衣服要洗, 于是满街找洗衣房。突然他们见到一扇窗户上有标记:『这里是洗衣房』。一个人高声问道: 『我们可以把衣服留在这儿让你洗吗?』窗内的老板回答说:『不, 我们不洗衣服。』来人又问道:『你们窗户上不是写着是洗衣房吗』。老板又回答说: 『我们是做洗衣房标记的, 不洗衣服』。这很有点像数学家。数学家们只做普遍适合的标记, 而物理学家却创造了大量的数学。」
杨振宁教授的故事是一则深刻的寓言。数学圈外的人们对数学家们「只做标记, 不洗衣服」的做法是不赞成的。数学家Ulam 在引了杨振宁的「笑话」之后, 问道, 信息论是工程师C. Shannon 创立的, 而纯粹数学家为什么不早就建立起来? 他感叹地说:「现今的数学和19世纪的数学完全不同, 甚至百分之九十九的数学家不懂物理。然而有许许多多的物理概念, 要求数学的灵感, 新的数学公式, 新的数学观念。」
二、理论物理的「猜」和数学的「证」
1995年12月, 杨振宁先生接到复旦大学校长杨福家的来信, 请杨振宁在1996年5月到复旦为「杨武之讲座」做首次演讲。杨武之教授是杨振宁的父亲, 又是中国数学前辈,早年任清华大学数学系系主任多年, 五十年代后则在复旦大学任教授, 所以杨振宁很愉快地接受了邀请。但是他不能像杨福家校长要求的那样做20次演讲, 只准备讲三次。顺着这一话题, 杨振宁先生又谈了理论物理和数学的一些关系。
杨先生说:「理论物理的工作是『猜』, 而数学讲究的是『证』。理论物理的研究工作是提出『猜想』, 设想物质世界是怎样的结构,只要言之成理, 不管是否符合现实, 都可以发表。一旦『猜想』被实验证实, 这一猜想就变成真理。如果被实验所否定, 发表的论文便一文不值(当然失败是成功之母,那是另一层意思了)。数学就不同, 发表的数学论文只要没有错误, 总是有价值的。因为那不是猜出来的, 而有逻辑的证明。逻辑证明了的结果, 总有一定的客观真理性。」
「正因为如此, 数学的结果可以讲很长的时间, 它的结果以及得出这些结果的过程都是很重要的。高斯给出代数学基本定理的五种证明, 每种证明都值得讲。如果让丘成桐从头来讲卡拉比(Calabi) 猜想的证明, 他一定会有20讲。但是教我讲『宇称不守恒』是怎么想出来的, 我讲不了多少话。因为当时我们的认识就是朝否定宇称守恒的方向想,『猜测』不守恒是对的。根据有一些, 但不能肯定。究竟对不对, 要靠实验。」
杨先生最后说:「理论物理的工作好多是做无用功, 在一个不正确的假定下猜来猜去,文章一大堆, 结果全是错的。不像数学, 除了个别错的以外, 大部分都是对的, 可以成立的」。
杨先生的这番话, 使我想起不久前Quine 和Jaffe 的一篇文章, 发表于Bulletin of AMS,1993年8月号, 曾引起相当的轰动。该文的主题是问「猜测数学是否允许存在? 」。其中提到, 物理学已经有了分工, 理论物理做「猜测」, 实验物理做「证明」。但是数学没有这种分工。一个数学家, 既要提出猜想, 又要同时完成证明。除了希尔伯特那样的大人物可以提出23个问题, 其猜想可以成为一篇大文章之外, 一般数学家至多在文章末尾提点猜想以增加读者的兴趣, 而以纯粹的数学猜想为主体的文章是无处发表的。因此, 两位作者建议允许「理论数学」, 即「猜测数学」的存在。
这样一来, 现在有两种相互对立的看法。一方面, 物理学界中像杨振宁先生那样, 觉得理论物理的研究太自由, 胡乱猜测皆成文章,认为数学还比较好的。另一方面, 数学界如Quine 和Jaffe 那样, 觉得目前数学研究要求每个结论都必需证明的要求, 太束缚人的思想。应该允许人们大胆地猜测, 允许有根据而未经完全确认的数学结论发表出来。二者孰是孰非, 看来需要一个平衡。许多问题涉及哲学和社会学层面, 就不是三言两语可以解决的了。
三、复数、四元数的物理意义

虚数i=p−1 的出现可溯源于15世纪时求解三次方程,但到18世纪的欧拉时代,仍称之为「想象的数」(imaginary)。数学界正式接受它要到19世纪, 经Cauchy, Gauss, Riemann, Weierstrass 的努力, 以漂亮的复变量函数论赢得历史地位。至于在物理学领域, 一直认为能够测量的物理量只是实数,复数是没有现实意义的。尽管在19世纪, 电工学中大量使用复数, 有复数的动势, 复值的电流, 但那只是为了计算的方便。没有复数,也能算出来, 只不过麻烦一些而已。计算的最后结果也总是实数, 并没有承认在现实中有真有「复数」形态的电流。鉴于此, 杨振宁先生说, 直到本世纪初,情况仍没有多少改变。一个例证是创立量子电动力学的薛定谔(Schrodinger)。1926年初, 据考证, 他似乎已经得到现在我们熟悉的方程
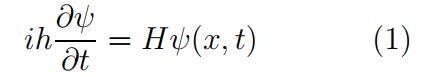
其中含有虚数单位i,是复函数, 但最后总是取实部。薛定谔因其中含虚数而对(1) 不满意, 力图找出不含复数的基本方程。于是他将上式两面求导后化简, 得到了一个没有虚数的复杂的高阶微分方程
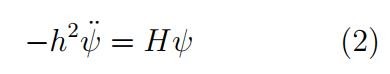
1926年的6月6日, 薛定谔在给洛兰兹的一封长信中, 认为这一不含复数的方程(2) 「可能是一个普遍的波动方程。」这时, 薛定谔正在为消除复数而努力。但是, 到了同年的6月23日, 薛定谔领悟到这是不行的。在论文[5]中,他第一次提出: 「 是时空的复函数, 并满足复时变方程(1)。」并把(1) 称谓真正的波动方程。其内在原因是, 描写量子行为的波函数, 不仅有振幅大小, 还有相位, 二者相互联系构成整体, 所以量子力学方程非用复数不可。另一个例子是H.Weyl 在1918年发展的规范理论, 被拒绝接受, 也是因为没有考虑相因子, 只在实数范围内处理问题。后来由Fock 和London 用加入虚数i 的量子力学加以修改, Weyl 的理论才又重新复活。20 数学传播21卷2期民86年6月牛顿力学中的量全都是实数量, 但到量子力学, 就必须使用复数量。杨振宁和米尔斯在1954年提出非交换规范场论, 正是注意到了这一点, 才会把Weyl 规范理论中的相因子推广到李群中的元素, 完成了一项历史性的变革。1959年, Aharanov 和Bohm 设计一个实验, 表明向量势和数量势一样, 在量子力学中都是可以测量的,打破了「可测的物理量必须是实数」的框框。这一实验相当困难,最后由日本的Tanomura 及其同事于1982和1986先后完成。这样, 物理学中的可测量终于扩展到了复数。
令我惊异的是, 杨振宁教授预言, 下一个目标将是四元数进入物理学。自从1843年爱尔兰物理学家和数学家Hamiton 发现四元数之后, 他本人曾花了后半辈子试图把四元数系统, 像复数系统那样地广泛运用于数学和物理学, 开创四元数的世纪。但结果是令人失望的。人们曾评论这是「爱尔兰的悲剧」。时至今日, 一个大学数学系的毕业生可能根本不知道有四元数这回事, 最多也不过是非交换代数的一个例子而已。我还记起,1986年春, 钱学森在致中国数学会理事长王元的一封信中, 曾建议多学计算器知识, 而把研究「四元数解析」(复变函数论的推广) 的工作贬为「像上一个世纪」东西。总之, 我和许多数学工作者一样, 认为四元数发现, 只不过是「抽象的数学产物」, 不会有什么大用处的。
杨振宁向我解释了他的想法: 物理学离不开对称。除了几何对称之外, 还有代数对称。试看四元数a+bi+cj+dk , 其基本单位满足i^2 = j^2 = k^2 = −1 , 而ij = k, jk =i , ki = j ; ij = −ji , jk = −kj , ki =−ik 。像这种对称的性质在物理学中经常可以碰到。问题是这种四元数的对称还没有真正用于物理现象, 而且物理现象中的一些对称也还没有找到基本的数学源由。最近, 丘成桐等人的文章说:「我在1977年发表的一篇文章—Condition of Self-duality for SU(2) gauge fields on Euclidean fourdimensionalspace, 曾推动代数几何中稳定丛的解析处理的理论。我还没有问过数学家, 不知道这是怎么一回事。许多工作, 包括运用四元数表示的物理理论, 也许会在这种交流中逐步浮现的」。
杨振宁先生又说, 至于将复变函数论形式地推广到四元数解析理论, 由于四元数乘积的非交换性, 导数无法唯一确定, 所以不会有什么好结果出来。现在也有物理学家写成著作, 用四元数来描写现有的物理定律, 就没有引起什么注意。将来要用四元数表达的物理定律, 一定会是一组非线性微分方程组, 其解的对称性必需用四元数来表示。所以, 杨先生相信:「爱尔兰的悲剧是会变成喜剧的」。
四、「双叶」比喻
数学和物理学的关系, 应该是十分密切的。在数学系以外的课程中, 物理系开设的数学课最多最深。「物理学公理化, 数学化」, 曾是一个时期许多大学问家追逐的目标。不过, 擅长使用数学于物理的杨振宁教授却认二者间的差别很大, 他有一个生动的「双叶」比喻, 来说明数学和物理学之间的关系, 如下图。他认为数学和物理学像一对「对生」的树叶, 他们只在基部有很小的公共部分, 多数部分则是相互分离的。杨振宁先生解释说: 「它们有各自不同的目标和价值判断准则, 也有不同的传统。在它们的基础概念部分, 令人吃惊地分享着若干共同的概念, 即使如此, 每个学科仍旧按着自身的脉络在发展。」
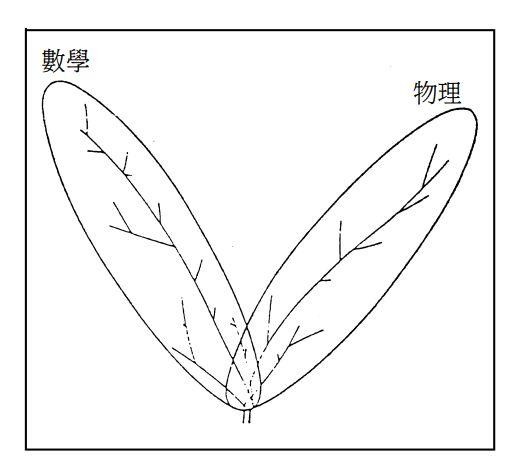
原文标题:和杨振宁教授漫谈: 数学和物理的关系,来自《数学传播》
本文作者:华东师范大学教授张奠宙先生
版权归原作者所有,若侵删
本文经授权转载自《超级数学建模》微信公众号
特别声明:以上文章内容仅代表作者本人观点,不代表新浪网观点或立场。如有关于作品内容、版权或其它问题请于作品发表后的30日内与新浪网联系。
网址:杨振宁教授漫谈:数学和物理的关系 https://mxgxt.com/news/view/320300
相关内容
杨振宁和钱学森到底是什么关系?百岁杨振宁,如何看待百年来数学与物理的分与合
杨振宁一家的混乱关系 翁帆父亲与杨振宁18 岁孙女喜结连理
杨振宁
特别策划:与杨振宁同时代的科学家们
96岁的杨振宁牵手42岁娇妻翁帆!揭秘其一家的混乱关系:孙女嫁给岳父
杨振宁披露与翁帆交往细节:那一年很特别
杨振宁与夫人杜致礼的婚姻:是科学灵魂与艺术灵魂的碰撞与结合
邓稼先与杨振宁 跨越半个世纪的友情
杨振宁去世