1.2 网络数据的相关指标
在网络数据分析中,需要关注一些重点指标,例如,一个网络的结构是围绕几个节点高度中心化,还是扁平的;网络中节点之间的联系是紧密还是松散的等。利用这些指标,不仅可以对网络特征进行定量化的描述,了解网络的具体特质,还可以为更深入分析任务提供帮助,如发现网络中内部联系紧密的小团体等。下面将对网络分析中常用指标进行具体介绍。
1.2.1 度的定义及度分布
对网络中的单个节点,度(degree)是描述节点属性最基础而又最重要的指标之一。在单模的无向网络中 中,对节点 ,度 表示与节点 直接相连的边的数目,如微信中的好友数。给定邻接矩阵 ,则节点 的度为 。在双模网络中,度 同样表示与节点 直接相连的边的数目。例如,对商户 而言, 表示在每个商户交易的用户总数;对用户 而言, 表示其交易过的商户总数。
对有向网络,节点的度可进一步分为出度(out-degree) 和入度(in-degree)。节点 的出度 表示从节点 指向其他节点的边的数目,即 ;入度 表示从其他节点指向节点 的数目,即 。如图1.7所示,对节点 ,仅有一条边指向它,因此节点 的入度为1;同时存在两条由 指向其他节点的边,因此 的出度为2。
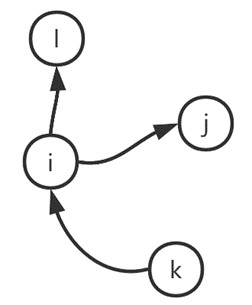
图1.7 出、入度示意图
节点的度是对网络局部单个节点性质的刻画。当计算得到网络中每个节点的度之后,即可得到整个网络在节点度上的分布。网络的度分布是网络整体性质的反映。此外,还可通过平均度(average degree) 对网络整体的度分布进行刻画。平均度为网络中所有节点的度的平均,即 。对出度、入度,可类似地定义平均出度、平均入度。平均度越高,则整体意义上网络中的边越密集,网络中节点间的联系越紧密。
通过节点的度,可以对节点在网络中的局部连接情况得到直观认识。例如在好友网络中,一个节点的度较高表明相应个体在人际交往中好友较多。而通过节点度的分布,则可以对网络整体有直观了解。例如一个度分布较为平均的好友网络,通常个体间存在扁平化的交往关系,即每个人的好友数量是相近的;而一个度分布非常不均衡的好友网络,则更可能是存在若干个”交际明星“,他们的好友数量明显高出一般人。
1.2.2 聚类系数
聚类系数(clustering coefficient)是对网络紧密程度的一种度量。以下分别介绍节点的聚类系数和网络的聚类系数。对单个节点 ,聚类系数反映了它的任意两个邻居节点之间存在边的概率。给定节点 的度 ,则节点 的聚类系数定义为
其中 是节点 的 个邻居节点彼此之间边的数目(不包括它们与节点 之间的边),即节点 邻居节点中,存在关联的邻居对的数目。若节点 没有或者仅有一个邻居节点,则 为0。节点聚类系数 取值范围为 。给定邻接矩阵 ,聚类系数 可通过下式计算:
对网络整体,网络的聚类系数定义为所有节点的聚类系数的平均,即
网络的聚类系数 越高,表明网络中的耦合程度越大。 的取值范围同样为 。当 时,网络中所有节点的聚类系数均为1,此时任意两个节点之间都是直接相连的。
例如,对图1.8构成的网络,考虑对节点 计算聚类系数。节点 周边存在6个节点,从而存在 个邻居对。15 对邻居节点相互之间存在4 条边。因此节点 的聚类系数即为 。以同样方式可得,其他节点的聚类系数为 ,整个网络的聚类系数即为 。
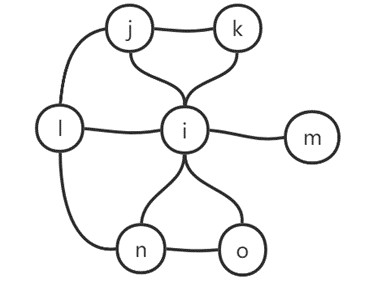
图1.8 聚类系数计算示例网络
通过聚类系数,可以对网络的紧密程度进行刻画。例如对一个好友网络,若聚类系数较高,则说明网络的个体之间相互连接紧密,许多个体拥有大量共同好友。而若聚类系数较低,则说明网络连接较为松散,存在更多的一对一的好友关系。
1.2.3 社区的定义
社区 (community) 一般指具有某些共同特征的人聚集在一起形成的组织。在社交网络分析中,社区通常表现为一种特征明显的结构:社区内部的节点相互连接较为紧密,而社区之间的节点连接相对稀疏。图1.9展示了一个简单的具有社区结构的网络,由虚线划分出的各部分为该网络内的各个社区。社区检测是社会网络分析中的一个重要研究课题,高效的社区检测方法能够对网络结构的刻画、人群属性细分、好友推荐等问题提供有力的支持。
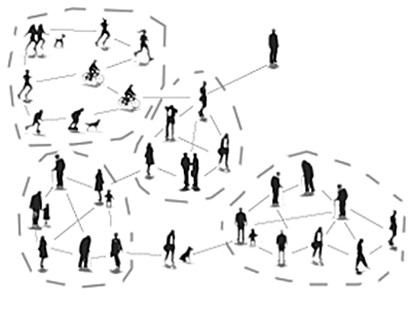
图 1.9 社区结构示意图
需要指出的是,社区的概念不仅包括人与人组成的群体,也能够在其他的网络数据中,描述由关联紧密的节点构成的组织结构。对社区结构的研究应用广泛,包括社会行为 (Fortunato, 2010)、蛋白质与蛋白质的相互作用(Chen and Yuan, 2006)、基因表达(Jiang et al., 2004)、推荐系统(Linden et al., 2003);图像分割(Shi and Malik, 2000)、产品-客户细分(Clauset et al., 2004)、网页排序(Kumar et al., 1999)等不同的网络数据分析。例如,在基因表达中,“社区”可以是在功能上具有密切关联的一群蛋白,研究者在分析生物性质时,可以将这一“社区”作为一个功能单元来考察;在图像分割中,“社区”可以是相关性高的一群像素点,表示一个特定的物体对象;在网页排序中,“社区”可以是一组相互间存在大量超链接的网页,这些网页在语义上或信息资源共享上关联更大,当用户浏览其中一个网页时,相比一般的网页,将更有可能跳转到“社区”内部的其他网页上。
1.2.4 中心性的定义
一个节点在网络中所处的位置也是对节点进行考察的重要指标。例如,在微博用户构成的社交网络中,处在关注焦点、粉丝数量较多的用户往往对整个网络具有更强的影响力。网络中位置越靠近中心的节点,通常具有更大的价值,或能够在信息扩散、网络演化中发挥更大的作用。为了描述节点在网络中的位置特征,社会网络分析中使用“中心性”(centrality)作为考察指标。根据刻画特征的倾向不同,中心性可进一步分为度中心性(degree centrality)、介数中心性(betweeness centrality)和接近中心性(closeness centrality)。以下分别对这几种中心性的定义进行介绍。
度中心性主要直观考察节点的度,一个节点的度越大,则它连接的节点越多,在网络中可能具有更大的价值。如图1.10所示,节点 i 在网络中具有很高的度,与之直接相连的节点较多,因此节点 i 度中心性较高,它能够直接影响很多节点。
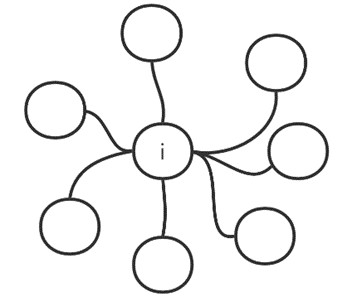
图1.10 度中心性示意图
定义1.8.(度中心性):对节点 ,度中心 性定义为
其中 为该节点的度, 为网络节点总数。
网络中的某些节点可能存在于其他众多节点间的通路上,从而体现出”中介“的功能。例如对一个职场人士构成的网络,公司 和公司 是两个相对独立的公司,旗下员工之间联系非常少,而猎头 和两个公司的大部分员工都建立了社交联系。那么猎头 在这个网络中也具有很强的影响力。两个公司间的员工如果想要建立直接的合作联系,则需要猎头 提供中介支持。又例如对交通网络,网络中的桥梁、隧道节点对整个交通网的管理具有重要价值,因为许多节点之间的互联互通需要通过这些桥梁、隧道。这种中心性称为”介数中心性“,介数中心性较高的节点,往往在网络中具有”牵一发而动全身“的作用。图1.11为介数中心性提供了一个直观的说明,图中节点 处在两个内部连接较为紧密社群之间,将两个社群联系在一起,节点 在该网络中具有较高的介数中心性。
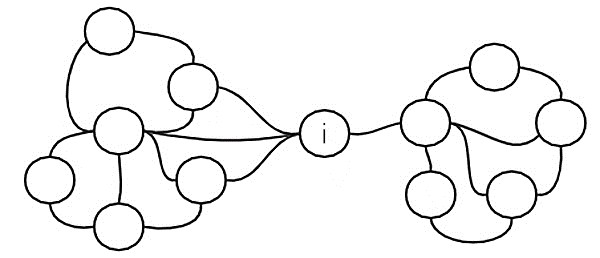
图1.11 介数中心性示意图
在介绍介数中心性的具体定义之前,首先需要说明路径和最短路径的概念。图1.12展示了一个关于路径的简单例子。从节点 到节点 存在两条”通路“: 和 。这两条通路都是从节点 到节点 的路径。同时,通路 只经过两条连边,而通路 则需要经过三条连边。因此,在这两条路径中, 是最短路径。下面将给出路径和最短路径的具体定义。
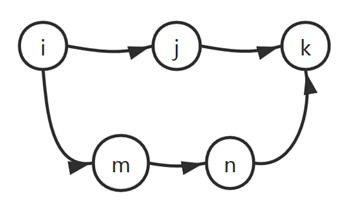
图1.12 路径与最短路径
定义1.9.(路径):对节点 与节点 ,若它们相邻,则边 即为它们间的路径。若不相邻,则连接 与 的路径为一组连接这两个节点的边的集合 。
节点 与节点 之间的路径可能不止一条,在这些路径中,构成的边数量最少的路径即为最短路径。
定义1.10.(最短路径):对节点 与节点 ,最短路径为 。
在实际网络中,两个节点之间的最短路径同样可能不止一条。基于最短路径的概念,可对介数中心性的定义进行说明。
定义1.11.(介数中心性):对节点 ,介数中心性的具体定义为
其中,表示节点与之间最短路径的数量,表示节点和之间条最短路径中,经过了节点的路径数量。
在度中心性中,考察的是直接相连的节点数目,而实际网络的节点间存在大量的间接关联,这些间接的联系并没有得到妥善考虑。接近中心性则通过计算节点到网络中所有其他节点的平均距离来衡量节点靠近网络中心的程度,同时考虑了节点之间直接和间接的关联。例如在一个微博用户构成的网络中,用户 直接相有关联的用户数量较少,但是用户 和明星用户 、 为相互关注的好友,由于 、 通过粉丝关注的关系与大量用户直接关联,因此用户 在网络中距离其他所有节点的平均距离相对较小。从整体来看,该用户可通过 、 间接影响到大量用户,也对整个网络具有可观的影响力。如图1.13所示,节点 在网络中直接相连的节点、间接相连的节点均较多,从节点 到其他任意节点最多只需要两次连接,因而节点 具有较高的接近中心性。
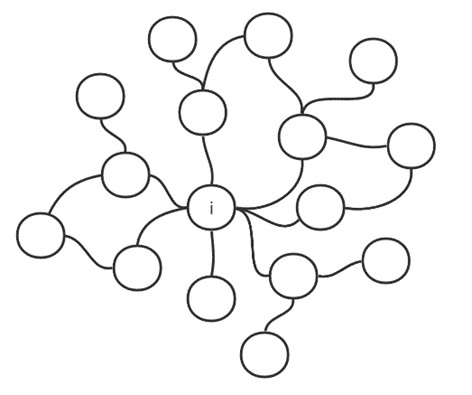
图1.13 接近中心性示意图
定义1.12.(接近中心性):对节点 ,接近中心性定义为
其中 表示节点 和 之间的最短路径距离。
参考文献
Chen, J. and Yuan, B. (2006), “Detecting functional modules in the yeast protein-protein interaction network,” Bioinformatics, 22, 2283–2290.
Clauset, A., Newman, M. E. J., and Moore, C. (2004), “Finding community structure in very large networks,” Physical Review E, 70, 066111.
Fortunato, S. (2010), “Community detection in graphs,” Physics Reports, 486, 75–174.
Jiang, D., Tang, C., and Zhang, A. (2004), “Cluster analysis for gene expression data: a survey,” IEEE Transactions on Knowledge and Data Engineering, 16, 1370–1386.
Kumar, R., Raghavan, P., Rajagopalan, S., and Tomkins, A. (1999), “Trawling the web for emerging cyber-communities,” Computer Networks, 31, 1481–1493.
Linden, G., Smith, B., and York, J. (2003), “Amazon. com recommendations: Item-to-item collaborative filtering,” IEEE Internet Computing, 7, 76–80.
Shi, J. and Malik, J. (2000), “Normalized cuts and image segmentation,” IEEE Transactions on pattern analysis and machine intelligence, 22, 888–905.
作者简介
黄丹阳,中国人民大学统计学院副教授,博士生导师,应用统计科学研究中心研究员,中国人民大学杰出青年学者,北京大数据协会理事会副秘书长,常务理事,全国工业统计学教学研究会青年统计学家协会理事。主持国家自然科学基金面上项目,青年项目,北京市社会科学基金青年项目等多项省部级及以上课题,曾获北京市优秀人才培养资助。长期从事复杂网络建模、超高维数据分析、分布式计算等方向的理论研究工作,注重统计理论研究在小微企业数字化发展中的实际应用。在Journal of Econometrics, Journal of the American Statistical Association, Journal of Business & Economic Statistics,以及《统计研究》等国内外期刊发表论文近30篇。
书籍简介
本书的主要内容包括网络数据的基本定义及基本特征,大规模网络数据的常见分析方法(链路预测,网络聚类)及应用,以及空间自回归模型在网络数据分析中的定义,模型拓展以及应用等等。本书关注大规模网络数据分析中的模型方法。除模型方法本身的理论拓展之外,在估计方法等方面会涉及大规模数据中的快速计算方法。由于网络分析本身的范围非常广泛,故本书涉及到的仅局限于作者及团队研究工作中使用到的一部分。在书的最后,为了启发读者思路,本书对于部分已有网络研究进行了梳理。本书的读者对象为统计学学者,对网络数据分析感兴趣,并且具备一定统计学基础的研究生,高年级本科生等。
扫描以下二维码购买本书:
往期推荐:
第1章 网络数据的定义及相关指标 (1) 返回搜狐,查看更多
责任编辑:

