自动机

理性愉悦之自动机专题确定有限状态自动机AC 自动机构建字典树构建构建失配指针构建转移函数一些有用的性质例题及应用多模匹配P5357 【模板】AC 自动机（二次加强版）P5231 [JSOI2012]玄武密码P3966 [TJOI2013]单词P2444 [POI2000] 病毒P2322 [HNOI2006]最短母串问题P4052 [JSOI2007]文本生成器BZOJ 2905 背单词P4045 [JSOI2009] 密码[BJWC2011]禁忌SAM——后缀自动机

理性愉悦之自动机专题

确定有限状态自动机

以下内容引用自 OI-wiki：

一个 确定有限状态自动机（DFA） 由以下五部分构成

字符集（Σ" role="presentation">Σ），该自动机只能输入这些字符 状态集合（Q" role="presentation">Q）。如果把一个 DFA 看成一张有向图，那么 DFA 中的状态就相当于图上的顶点 起始状态（start" role="presentation">start），start∈Q" role="presentation">start∈Q，是一个特殊的状态。 接受状态集合（F" role="presentation">F），F⊆Q" role="presentation">F⊆Q，是一组特殊的状态 转移函数（δ" role="presentation">δ），δ" role="presentation">δ 是一个接受两个参数返回一个值的函数，其中第一个参数和返回值都是一个状态，第二个参数是字符集中的一个字符。如果把一个 DFA 看成一张有向图，那么 DFA 中的转移函数就相当于顶点间的边，而每条边上都有一个字符。

当一个 DFA 读入一个字符串时，从初始状态起按照转移函数一个一个字符地转移。如果读入完一个字符串的所有字符后位于一个接受状态，那么我们称这个 DFA 接受 这个字符串，反之我们称这个 DFA 不接受 这个字符串。

如果一个状态 v" role="presentation">v 没有字符 c" role="presentation">c 的转移，那么我们令 δ(v,c)=null" role="presentation">δ(v,c)=null，而 null" role="presentation">null 只能转移到 null" role="presentation">null，且 null" role="presentation">null 不属于接受状态集合。无法转移到任何一个接受状态的状态都可以视作 null" role="presentation">null，或者说，null" role="presentation">null 代指所有无法转移到任何一个接受状态的状态。

AC 自动机

kmp 算法只能处理单模式串的字符串匹配，如果要处理多个模式串的字符串匹配，运行多遍kmp显然不现实，但我们发现可以将处理多字符串的 Trie 树与 kmp 的失配指针结合一下，AC自动机应运而生

构建

字典树构建

AC 自动机建立时，先把模式串都丢进一个 Trie 里，所以对于 AC 自动机里的结点的状态的意义自然与 Trie 树的一样——某（些）个模式串的前缀，发现一个状态可以存在于多个模式串中，这就是 AC 自动机能匹配多模式串的前提

构建失配指针

AC 自动机的失配指针定义如下：

对于一个状态 p" role="presentation">p 的失配指针 fail" role="presentation">fail 来说，它指向的是一个状态 q" role="presentation">q，满足 q" role="presentation">q 是所有状态中 p" role="presentation">p 的最长后缀

AC 自动机的失配指针与 kmp 的相似之处：都是失配时用于跳转避免重复匹配
不同之处：kmp 是求最长公共前后缀（自己匹配自己），AC 自动机是所有状态的最长公共后缀状态（自己匹配所有）

所以构建的时候也可以借助 kmp 的思想

设当前结点为 u" role="presentation">u，其父节点为 p" role="presentation">p，p" role="presentation">p 通过字符为的 c" role="presentation">c 边连向 u" role="presentation">u

如果 failp" role="presentation">failp 处存在字符为 c" role="presentation">c 的 Trie 树边，那么 u" role="presentation">u 的失配指针即为这条边指向的结点 如果 1 不成立，令 p=failp" role="presentation">p=failp 继续进行 1 如果 p" role="presentation">p 走到了根节点，那么使 failu" role="presentation">failu 指向根节点 构建转移函数

对于上述构建失配指针的算法显然是不优的，而对于任何状态转移函数 δ(s,c)" role="presentation">δ(s,c) 都应有值，所以考虑不仅求出 Trie 树及其失配指针，还求出其所有的状态转移函数

对于存在于 Trie 树上的边，状态转移函数即为这条边，如果不存在的话，考虑接受这个字符后最优会走到哪里，将要走到的是 δ(failp,c)" role="presentation">δ(failp,c) ，而如果这个转移函数不存在的话，这个转移函数会以相同的形式递归下去，直到有解或走到根节点，所以这个转移是 O(1)" role="presentation">O(1) 的

失配指针的构建也可以像这样给出特殊处理：failtriep,c=triefailp,i" role="presentation">failtriep,c=triefailp,i 其实就是利用上述的特殊处理省去了递归的过程

考虑到其用于转移的值一定来自于在 Trie 树上比当前点深度小的结点，所以使用bfs实现

时空复杂度为 O(∑|si|⋅|Σ|)" role="presentation">O(∑|si|⋅|Σ|)，si" role="presentation">si 为模式串

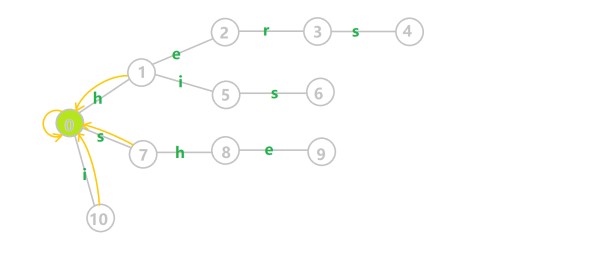
代码实现：

void build(){ queue<int> q; for(int i=0;i<26;i++) if(trie[0][i]) q.push(trie[0][i]); while(!q.empty()){ int u=q.front(); for(int i=0;i<26;i++){ if(trie[u][i]){ fail[trie[u][i]]=trie[fail[u]][i]; q.push(trie[u][i]); } else trie[u][i]=trie[fail[u]][i]; } q.pop(); } }

一些有用的性质

AC 自动机的性质集中在 fail 树之中，它有以下几点性质：

fail 树显然是一棵有根树，支持很多树上操作 对于一个状态 p" role="presentation">p 而言，其在 fail 树上的子树内的状态 x" role="presentation">x，都有 p" role="presentation">p 是 x" role="presentation">x 的后缀 如果一个状态 p" role="presentation">p 为终止状态，那么说明 p" role="presentation">p 的子树内状态均为终止状态，由 2 可得，子树内状态的结尾与当前状态相同，由此得证 作为当前状态 p" role="presentation">p 的单词数量为从当前状态到根节点的单词数量

例题及应用

多模匹配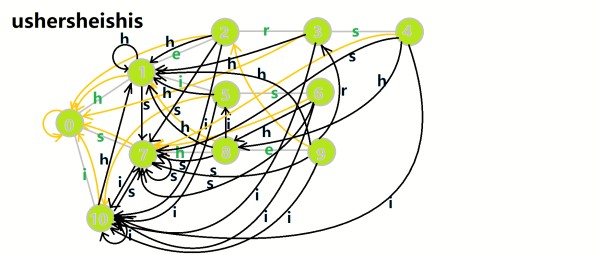

直接按着转移函数走即可

Code:

int query(string s,int len){ int u=0,ans=0; for(int i=1;i<=len;i++){ u=trie[u][s[i]-'a']; for(int j=u;j&&cnt[j]!=-1;j=fail[j]) ans+=cnt[j],cnt[j]=-1; } return ans; } P5357 【模板】AC 自动机（二次加强版）

统计模式串在文本串中出现的次数

跑一遍多模匹配，顺便搞出来每个结点被经过的次数，答案即为每个单词所对应的终止结点在 fail 树上子树结点被经过次数之和

P5231 [JSOI2012]玄武密码

先建好 AC 自动机，然后跑一遍多模匹配，在 fail 树上匹配 Trie 树深度的最大值则为答案

P3966 [TJOI2013]单词

对于每个串来说，先计算其在 Trie 树上覆盖的次数，建立 AC 自动机，然后计算其在 fail 树上的和即可

P2444 [POI2000] 病毒

好题

先建立 AC 自动机，在建立的时候更新一个结点是否能匹配上一个模式串，然后发现 AC 自动机是个图，如果从 Trie 树根节点开始，能不匹配上任何模式串走一个环就可以

P2322 [HNOI2006]最短母串问题

从此之后就是 AC 自动机上 dp 的题，主要套路为答案与字符串接龙有关，类似有向图上 dp

这道题看到数据范围果断状压，维护当前状态前一个字符和是否经历过当前状态，和每个字符串是否取到，然后 bfs 更新保证字典序最小即可

P4052 [JSOI2007]文本生成器

我的做法是搞两个数组，fi,j,gi,j" role="presentation">fi,j,gi,j 分别表示长度为 j" role="presentation">j，遍历到 AC 自动机 i" role="presentation">i 号结点的方案数，f" role="presentation">f 为不一定存在可读字符的方案数，g" role="presentation">g 为存在的方案数，只有 f" role="presentation">f 有初值，f" role="presentation">f 由 f" role="presentation">f转移得来，g" role="presentation">g 由 f" role="presentation">f 和 g" role="presentation">g 同时转移得来，f" role="presentation">f 能转移到 g" role="presentation">g 当且仅当目标结点能匹配上某个串，答案即为对 g" role="presentation">g 求和

似乎正常做法是正难则反

BZOJ 2905 背单词

如果该单词包含之前的单词，则后缀来自于 fail 树的祖先，枚举路径上的点，查询这条路径的最大值即为当前的答案，对于一个串来说，其对在 fail 树上的子树有影响，dfs 序维护线段树即可

P4045 [JSOI2009] 密码

大水题，直接套路状压 dp 即可

[BJWC2011]禁忌

这道题和这个很像，原因是 kmp 和 AC 自动机都有一个很相似的转移函数，可以直接用作随机/随便搞的字符串匹配矩阵来进行加速递推，这道题考虑每次到能匹配上的点时加上个常数即可

SAM——后缀自动机

先搁着

网址：自动机 http://mxgxt.com/news/view/924371

相关内容

【多功能自动售货机】
babystar 面条机家用手持式全自动无线压面机智能电动烙机多功能 149元
全自动铝材切割机
了解机器人与自动化之间的差异
SLAM+运动规划=机器人自主定位导航
国产红旗汽车的发动机究竟来自哪里？打开发动机盖后：这怎么可能
纵目之殇，从自动驾驶明星到经营危机
全自动切铝机出现毛边、毛刺如何解决？
ORIENT STAR 东方星 大师系列 自动机械男士腕表 RE
全自动人形饭撒机上线 超温柔飞吻again&again ffzeromile

随便看看